Xét tính liên tục của các hàm số sau trên TXĐ của chúng
f(x)= {x2-3x +4 khi x<2
{ 5 khi x=2
{2x +1 khi x>2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
6 tháng 2 2018
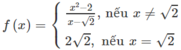
Tập xác định của hàm số là D = R
- Nếu x ≠ √2 thì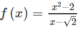 
Đây là hàm phân thức hữu tỉ nên liên tục trên các khoảng (-∞; √2) và (√2; +∞)
- Tại x = √2:
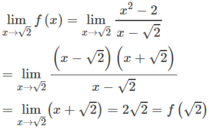
Vậy hàm số liên tục tại x = √2
Kết luận : y = f(x) liên tục trên R
CM
20 tháng 9 2018
Xét tính liên tục của hàm số sau trên tập xác định của nó:
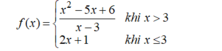
● Hàm số liên tục với mọi x ≠ 3.
● Tại x = 3, ta có:
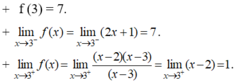
⇒ Hàm số không liên tục tại x = 3.
- Vậy hàm số liên tục trên các khoảng (-∞ ; 3), (3 ; +∞).
CM
10 tháng 3 2017
Chọn B.
Hàm số có nghĩa khi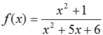 
.
Vậy theo định lí ta có hàm số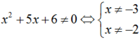 
liên tục trên khoảng (-∞; -3); (-3; -2) và (-2; +∞).
`TXĐ: R`
`@` Nếu `x > 2` thì: `f(x)=2x+1`
H/s xác định trên `(2;+oo)`
`=>` H/s liên tục trên `(2;+oo)`
`@` Nếu `x < 2` thì: `f(x)=x^2-3x+4`
H/s xác định trên `(-oo;2)`
`=>` H/s liên tục trên `(-oo;2)`
`@` Nếu `x=2` thì: `f(x)=5`
`lim_{x->2^[-]} (x^2-3x+4)=2`
`lim_{x->2^[+]} (2x+1)=5`
Vì `lim_{x->2^[-]} f(x) ne lim_{x->2^[+]} f(x) =>\cancel{exists} lim_{x->2} f(x)`
`=>` H/s gián đoạn tại `x=2`
KL: H/s liên tục trên `(-oo;2)` và `(2;+oo)`
H/s gián đoạn tại `x=2`