Giải các phương trình nghiệm nguyên sau:
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 12 2021
\(\Leftrightarrow23x+53y=23.37-53.14\)
\(\Leftrightarrow53y+53.14=23.37-23x\)
\(\Leftrightarrow53\left(y+14\right)=23\left(37-x\right)\)
Do 53 và 23 nguyên tố cùng nhau \(\Rightarrow y+14⋮23\)
\(\Rightarrow y+14=23k\Rightarrow y=23k-14\)
\(\Rightarrow x=-53k+37\)
Vậy nghiệm của pt là \(\left(x;y\right)=\left(-53k+37;23k-14\right)\) với \(k\in Z\)
CM
18 tháng 11 2017
Thay x = 3, y = 5 vào vế trái của phương trình (3) ta được:
VT = 5.3 – 2.5 = 15 – 10 = 5 = VP
Vậy (x; y) = (3; 5) là nghiệm của phương trình (3).
Hệ phương trình đã cho có nghiệm (x; ) = (3; 5)
23 tháng 9 2021
Ta có: \(3x+19y=168\)
\(\Rightarrow3x=168-19y\Rightarrow x=56-\dfrac{19y}{3}\)
Để \(x\in Z\Leftrightarrow19y⋮3\Leftrightarrow y⋮3\)
\(\Rightarrow y=3t\left(t\in Z\right)\)
Khi đó \(x=56-19t\)
Vậy \(\left(x;y\right)\in\left\{56-19t;3t\right\}\left(t\in Z\right)\)
CM
2 tháng 3 2019
Thay x = -3, y = 31/5 vào vế trái của phương trình (2), ta được:
VT = -3.(-3) + 2.31/5 = 9 + 62/5 = 107/5 ≠ 22 = VP
Vậy (x; y) = (-3; 31/5 ) không phải là nghiệm của phương trình (2).
Hệ phương trình đã cho vô nghiệm.
DT
3
30 tháng 5 2016
\(2xy-4x-y=1\Rightarrow2xy-4x-y+2=3\Rightarrow2x\left(y-2\right)-\left(y-2\right)=3\Rightarrow\left(2x-1\right)\left(y-2\right)=3\)
Vì x,y là nghiệm nguyên nên ta xét các trường hợp :
1. \(\hept{\begin{cases}2x-1=1\\y-2=3\end{cases}\Leftrightarrow\hept{\begin{cases}x=1\\y=5\end{cases}}}\)
2. \(\hept{\begin{cases}2x-1=3\\y-2=1\end{cases}\Leftrightarrow}\hept{\begin{cases}x=2\\y=3\end{cases}}\)
3. \(\hept{\begin{cases}2x-1=-1\\y-2=-3\end{cases}\Leftrightarrow\hept{\begin{cases}x=0\\y=-1\end{cases}}}\)
4. \(\hept{\begin{cases}2x-1=-3\\y-2=-1\end{cases}\Leftrightarrow}\hept{\begin{cases}x=-1\\y=1\end{cases}}\)
Vậy nghiệm của phương trình là : \(\left(x;y\right)=\left(-1;1\right);\left(0;-1\right);\left(1;5\right);\left(2;3\right)\)
30 tháng 5 2016
2xy-4x-y=1
x(2y-4)-y=1
2x(2y-4)-2y=2
2x(2y-4)-2y+4=6
2x(2y-4)-(2y-4)=6
(2y-4)(2x-1)=6
Đến đây, ta thấy 2x-1 là ước lẻ của 6 =>2x-1 E { 1;3 }
Với 2x-1=1 thì 2y-4=6 =>x=1, y=5
Với 2x-1=3 thì 2y-4=2 =>x=2, y=3
Em mới học lớp 6 nên chỉ làm theo cách lớp 6 thôi. Còn nghiệm nguyên thì em chưa học
LV
1
24 tháng 9 2021
Ta có: \(2x+3y=11\Leftrightarrow x=\frac{11-3y}{2}=5-y+\frac{1-y}{2}\).
Vì \(x\) và \(y\) nguyên nên \(\frac{1-y}{2}\) nguyên. Đặt \(\frac{1-y}{2}=t\left(t\inℤ\right)\)
\(\Rightarrow y=1-2t\)
\(\Rightarrow x=5-\left(1-2t\right)+\frac{1-\left(1-2t\right)}{2}=5-1+2t+t=3t+4\).
Vậy nghiệm của phương trình trên là: \(\hept{\begin{cases}x=3t+4\\y=-2t+1\end{cases}}\left(t\inℤ\right)\).
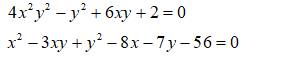
\(4xy+5x+y=-1\)
\(\Leftrightarrow y\left(4x+1\right)+\dfrac{5}{4}\left(4x+1\right)-\dfrac{5}{4}=-1\)
\(\Leftrightarrow4y\left(4x+1\right)+5\left(4x+1\right)-5=-4\)
\(\Leftrightarrow\left(4x+1\right)\left(4y+5\right)=1\)
Vì x,y là các số nguyên nên (4x+1), (4y+5) là các ước số của 1.
Lập bảng
Vậy phương trình đã cho có nghiệm (x,y) nguyên duy nhất là (0;-1).