Giúp tui câu a với nhaaa ~ Rất cảm ơnn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HP
24 tháng 10 2021
PTHH:
Fe + 2HCl ---> FeCl2 + H2
Cu + HCl ---x--->
Ta có: \(n_{H_2}=\dfrac{4,48}{22,4}=0,2\left(mol\right)\)
Theo PT: \(n_{Fe}=n_{H_2}=0,2\left(mol\right)\)
=> \(m_{Fe}=0,2.56=11,2\left(g\right)\)
=> \(\%_{m_{Fe}}=\dfrac{11,2}{15,6}.100\%=71,79\%\)
=> \(\%_{m_{Cu}}=100\%-71,79\%=28,21\%\)
24 tháng 10 2021
\(n_{H_2}=\dfrac{4,48}{22,4}=0,2mol\)
\(Fe+2HCl\rightarrow FeCl_2+H_2\)
0,2 0,2
\(m_{Fe}=0,2\cdot56=11,2\left(g\right)\) \(\Rightarrow\%m_{Fe}=\dfrac{11,2}{15,6}\cdot100\%\approx71,8\%\)
\(\Rightarrow\%m_{Cu}=100\%-71,8\%=28,2\%\)
TP
1
25 tháng 12 2021
Bài 1:
a: Xét ΔAMB và ΔAMC có
AM chung
AB=AC
BM=CM
Do đó: ΔABM=ΔACM
Giúp với mng ơii! e cảm ơnn
giúp e với ạ e cảm ơnn
7 tháng 8 2021
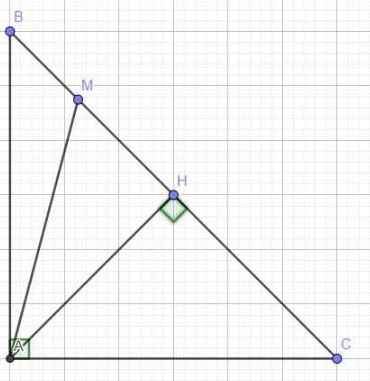
a)Kẻ AH⊥BC
Vì ΔABC vuông cân tại A
⇒ AH cũng là đường trung tuyến
⇒ AH=BH=CH
Ta có:MB2 + MC2 = (BH-HM)2 + (CH+HM)2 = (AH-HM)2+(AH+HM)2
= AH2-2.AH.HM+HM2+AH2+2.AH.HM+HM2=2(AH2+HM2)
Áp dụng định lý Py-ta-go vào ΔAHM vuông tại A ta có:
MA2 = AH2+HM2
⇒ MB2+MC2=2MA2
b) Ta có: MA≥AH (đường xiên và đường vuông góc)
⇒ MA2 ≥ AH2
⇒ 2MA2 ≥ 2AH2
⇒ MB2+MC2 ≥ 2AH2
Dấu "=" xảy ra ⇔ MA=AH ⇔ M là trung điểm của BC
Vậy Min K = 2AH2 ⇔ M là trung điểm của BC
\(\dfrac{\pi}{2}< a< \pi\Rightarrow cosa< 0\Rightarrow cosa=-\sqrt{1-sin^2a}=-\dfrac{4}{5}\)
\(\Rightarrow tana=\dfrac{sina}{cosa}=-\dfrac{3}{4}\)
\(tan\left(a+\dfrac{\pi}{3}\right)=\dfrac{tana+tan\dfrac{\pi}{3}}{1-tana.tan\dfrac{\pi}{3}}=\dfrac{-\dfrac{3}{4}+\sqrt{3}}{1-\left(-\dfrac{3}{4}\right).\sqrt{3}}=\dfrac{48-25\sqrt{3}}{11}\)
Em cảm ơn ạ ^^