
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1: Khi x=3-2 căn 2 thì \(A=\dfrac{\sqrt{2}-1+2}{\sqrt{2}-1}=\dfrac{\sqrt{2}+1}{\sqrt{2}-1}=3+2\sqrt{2}\)
2: \(B=\dfrac{x+\sqrt{x}+2+\sqrt{x}-2}{x-4}=\dfrac{x+2\sqrt{x}}{x-4}=\dfrac{\sqrt{x}}{\sqrt{x}-2}\)
3: \(P=A:B=\dfrac{\sqrt{x}+2}{\sqrt{x}}:\dfrac{\sqrt{x}}{\sqrt{x}-2}=\dfrac{x-4}{x}\)
\(x\cdot P< =10\sqrt{x}-29-\sqrt{x-25}\)
=>\(x-4< =10\sqrt{x}-29-\sqrt{x-25}\)
\(\Leftrightarrow x-4-10\sqrt{x}+29< =-\sqrt{x-25}\)
=>\(x-10\sqrt{x}+25< =-\sqrt{x-25}\)
=>(căn x-5)^2<=-căn x-25
=>x-25=0
=>x=25


a.
Khi \(x=4\Rightarrow A=\dfrac{1}{\sqrt{4}}+\dfrac{\sqrt{4}}{\sqrt{4}+1}=\dfrac{1}{2}+\dfrac{2}{3}=\dfrac{7}{6}\)
b.
\(B=\dfrac{1}{3}\Rightarrow\dfrac{\sqrt{x}}{x+\sqrt{x}}=\dfrac{1}{3}\)
\(\Rightarrow3\sqrt{x}=x+\sqrt{x}\)
\(\Rightarrow x-2\sqrt{x}=0\)
\(\Rightarrow\sqrt{x}\left(\sqrt{x}-2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}\sqrt{x}=0\\\sqrt{x}=2\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=0\left(ktm\right)\\x=4\left(tm\right)\end{matrix}\right.\)
c.
\(P=A:B=\left(\dfrac{1}{\sqrt{x}}+\dfrac{\sqrt{x}}{\sqrt{x}+1}\right):\left(\dfrac{\sqrt{x}}{x+\sqrt{x}}\right)\)
\(=\left(\dfrac{\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}+1\right)}+\dfrac{x}{\sqrt{x}\left(\sqrt{x}+1\right)}\right):\left(\dfrac{\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+1\right)}\right)\)
\(=\dfrac{\left(x+\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}+1\right)}.\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\sqrt{x}}=\dfrac{x+\sqrt{x}+1}{\sqrt{x}}\)
\(P>3\Rightarrow\dfrac{x+\sqrt{x}+1}{\sqrt{x}}>3\)
\(\Leftrightarrow x+\sqrt{x}+1>3\sqrt{x}\) (do \(\sqrt{x}>0\))
\(\Leftrightarrow x-2\sqrt{x}+1>0\)
\(\Leftrightarrow\left(\sqrt{x}-1\right)^2>0\)
\(\Leftrightarrow\sqrt{x}-1\ne0\)
\(\Rightarrow x\ne1\)
Kết hợp ĐKXĐ ta được: \(\left\{{}\begin{matrix}x>0\\x\ne1\end{matrix}\right.\)
anh ơi https://hoc24.vn/cau-hoi/giai-phuong-trinh-nghiem-nguyen-saux2x-y20.1353640161947
-> giải thích hộ cái bảng của a tính thế nào vs ạ

Câu 1:
Thay x=0 vào y=x+1, ta được:
y=0+1=1
Thay y=0 vào y=x+1, ta được:
x+1=0
hay x=-1
vậy: A(-1;0); B(0;1)
\(AB=\sqrt{\left(-1-0\right)^2+\left(0-1\right)^2}=\sqrt{2}\)
\(C_{OAB}=OA+OB+AB=2+\sqrt{2}\)
\(S_{OAB}=\dfrac{OA\cdot OB}{2}=\dfrac{1}{2}\)


a: \(x=2\sqrt{2}+2-2\sqrt{2}+2=4\)
Thay x=4 vào B, ta được:
\(B=\dfrac{2-3}{2+1}=\dfrac{-1}{3}\)

\(K=\dfrac{2\sqrt{3a+1}+2\sqrt{3b+1}+2\sqrt{3c+1}}{2}\)\(\le\)\(\dfrac{3a+1+4+3b+1+4+3c+1+4}{4}=\dfrac{24}{4}=6\)
Vậy \(K_{max}=6\)
Dấu bằng xảy ra khi a=b=c=1
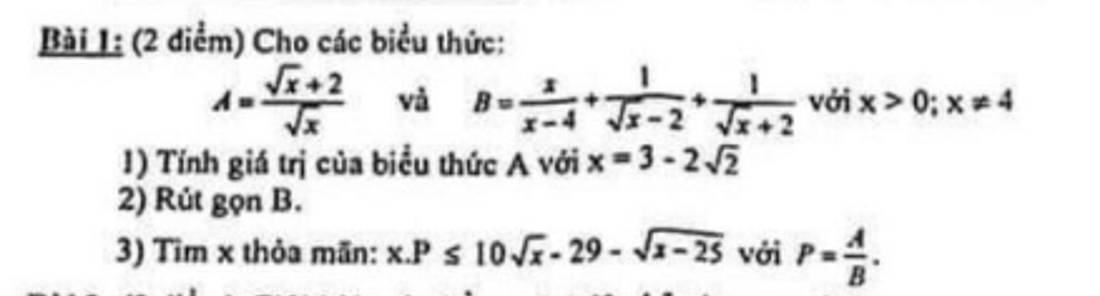
 Giúp với mng ơii! e cảm ơnn
Giúp với mng ơii! e cảm ơnn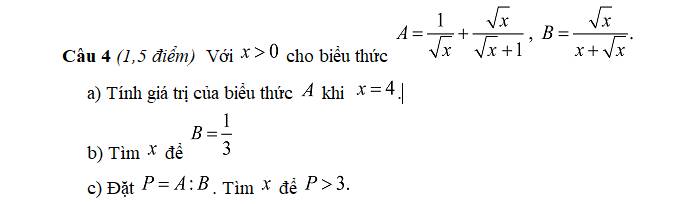

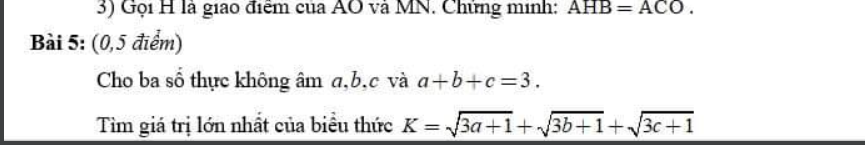
a)Kẻ AH⊥BC
Vì ΔABC vuông cân tại A
⇒ AH cũng là đường trung tuyến
⇒ AH=BH=CH
Ta có:MB2 + MC2 = (BH-HM)2 + (CH+HM)2 = (AH-HM)2+(AH+HM)2
= AH2-2.AH.HM+HM2+AH2+2.AH.HM+HM2=2(AH2+HM2)
Áp dụng định lý Py-ta-go vào ΔAHM vuông tại A ta có:
MA2 = AH2+HM2
⇒ MB2+MC2=2MA2
b) Ta có: MA≥AH (đường xiên và đường vuông góc)
⇒ MA2 ≥ AH2
⇒ 2MA2 ≥ 2AH2
⇒ MB2+MC2 ≥ 2AH2
Dấu "=" xảy ra ⇔ MA=AH ⇔ M là trung điểm của BC
Vậy Min K = 2AH2 ⇔ M là trung điểm của BC