
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


2:
1+cot^2a=1/sin^2a
=>1/sin^2a=1681/81
=>sin^2a=81/1681
=>sin a=9/41
=>cosa=40/41
tan a=1:40/9=9/40

\(\Leftrightarrow n^5+n^2-n^2+1⋮n^3+1\)
\(\Leftrightarrow-n^3+n⋮n^3+1\)
\(\Leftrightarrow n=1\)

\(\Leftrightarrow\left\{{}\begin{matrix}5x=10\\2x-y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=2x-3=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=2x-3\\3x+2x-3=7\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=2x-3\\5x=10\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=2.2-3\\x=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=1\\x=2\end{matrix}\right.\)

Gọi số học sinh nam là x
Số học sinh nữ là 32-x
Vì khi chuyển 4 nữ đi thì số nam và số nữ bằng nhau nên ta có:
32-x-4=x
=>28-x=x
=>x=14
Vậy: Có 14 nam và 18 nữ


a,\(\Delta=3^2-4\left(-2\right).6=9+48=57\)
\(x_1=\dfrac{-3+\sqrt{57}}{-4}=\dfrac{3-\sqrt{57}}{4}\)
\(x_2=\dfrac{-3-\sqrt{57}}{-4}=\dfrac{3+\sqrt{57}}{4}\)
b, \(\Delta=6^2-4.3.3=36-36=0\)
\(\Rightarrow x_1=x_2=\dfrac{-6}{2.3}=\dfrac{-6}{6}=-1\)
c, \(\Delta=1^2-4.6.5=1-120=-119< 0\)
Vậy pt vô nghiệm

a) \(=\sqrt{\left(\sqrt{5}+\sqrt{3}\right)^2}=\sqrt{5}+\sqrt{3}\)
b) \(=\sqrt{\left(\sqrt{2}+1\right)^2}=\sqrt{2}+1\)
c) \(=\sqrt{\left(2\sqrt{2}+3\right)^2}=2\sqrt{2}+3\)
d) \(=\sqrt{\left(3-\sqrt{5}\right)^2}=3-\sqrt{5}\)
e) \(=\sqrt{\left(4-\sqrt{6}\right)^2}=4-\sqrt{6}\)
f) \(=\sqrt{\left(3+\sqrt{7}\right)^2}=3+\sqrt{7}\)
l) \(=\sqrt{\left(\sqrt{2}-\dfrac{1}{2}\right)^2}=\sqrt{2}-\dfrac{1}{2}\)
m) \(=\sqrt{\left(2\sqrt{2}+\dfrac{1}{4}\right)^2}=2\sqrt{2}+\dfrac{1}{4}\)

\(=\sqrt{7-2\sqrt{21}+3}+\sqrt{7+2\sqrt{21}+3}\)
\(=\sqrt{\sqrt{7}^2-2\sqrt{7}.\sqrt{3}+\sqrt{3}^2}+\sqrt{\sqrt{7}^2+2\sqrt{7}.\sqrt{3}+\sqrt{3}^2}\)
\(=\sqrt{\left(\sqrt{7}-\sqrt{3}\right)^2}+\sqrt{\left(\sqrt{7}+\sqrt{3}\right)^2}\)
\(=\left|\sqrt{7}-\sqrt{3}\right|+\left|\sqrt{7}+\sqrt{3}\right|\)
\(=\sqrt{7}-\sqrt{3}+\sqrt{7}+\sqrt{3}\)
\(=2\sqrt{7}\)
\(\sqrt{10-2\sqrt{21}}+\sqrt{10+2\sqrt{21}}\)
\(=\sqrt{7}-\sqrt{3}+\sqrt{7}+\sqrt{3}\)
\(=2\sqrt{7}\)
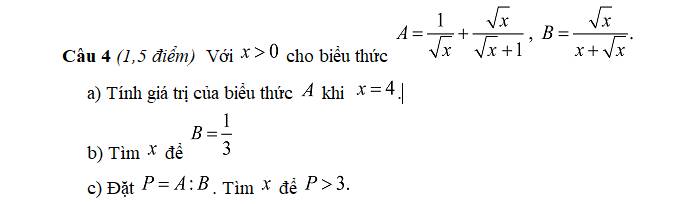



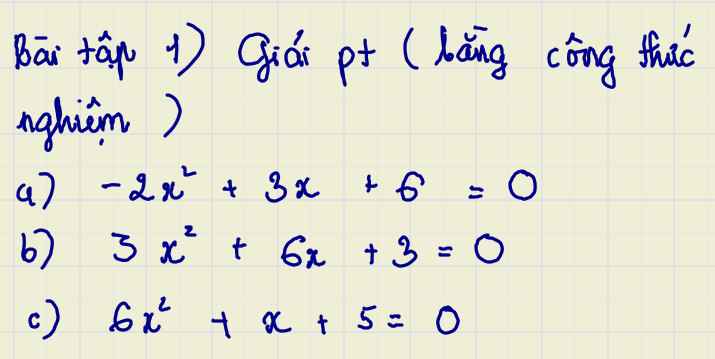
 Giúp mình bài này với ạ, mình cần lời giải chi tiết. Mình cảm ơn
Giúp mình bài này với ạ, mình cần lời giải chi tiết. Mình cảm ơn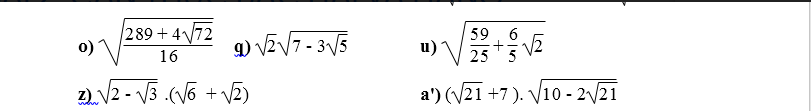
a.
Khi \(x=4\Rightarrow A=\dfrac{1}{\sqrt{4}}+\dfrac{\sqrt{4}}{\sqrt{4}+1}=\dfrac{1}{2}+\dfrac{2}{3}=\dfrac{7}{6}\)
b.
\(B=\dfrac{1}{3}\Rightarrow\dfrac{\sqrt{x}}{x+\sqrt{x}}=\dfrac{1}{3}\)
\(\Rightarrow3\sqrt{x}=x+\sqrt{x}\)
\(\Rightarrow x-2\sqrt{x}=0\)
\(\Rightarrow\sqrt{x}\left(\sqrt{x}-2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}\sqrt{x}=0\\\sqrt{x}=2\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=0\left(ktm\right)\\x=4\left(tm\right)\end{matrix}\right.\)
c.
\(P=A:B=\left(\dfrac{1}{\sqrt{x}}+\dfrac{\sqrt{x}}{\sqrt{x}+1}\right):\left(\dfrac{\sqrt{x}}{x+\sqrt{x}}\right)\)
\(=\left(\dfrac{\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}+1\right)}+\dfrac{x}{\sqrt{x}\left(\sqrt{x}+1\right)}\right):\left(\dfrac{\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+1\right)}\right)\)
\(=\dfrac{\left(x+\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}+1\right)}.\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\sqrt{x}}=\dfrac{x+\sqrt{x}+1}{\sqrt{x}}\)
\(P>3\Rightarrow\dfrac{x+\sqrt{x}+1}{\sqrt{x}}>3\)
\(\Leftrightarrow x+\sqrt{x}+1>3\sqrt{x}\) (do \(\sqrt{x}>0\))
\(\Leftrightarrow x-2\sqrt{x}+1>0\)
\(\Leftrightarrow\left(\sqrt{x}-1\right)^2>0\)
\(\Leftrightarrow\sqrt{x}-1\ne0\)
\(\Rightarrow x\ne1\)
Kết hợp ĐKXĐ ta được: \(\left\{{}\begin{matrix}x>0\\x\ne1\end{matrix}\right.\)
anh ơi https://hoc24.vn/cau-hoi/giai-phuong-trinh-nghiem-nguyen-saux2x-y20.1353640161947
-> giải thích hộ cái bảng của a tính thế nào vs ạ