Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó: ΔABM=ΔACM


a: Xét ΔAMB và ΔAMC có
MA chung
MB=MC
AB=AC
=>ΔAMB=ΔAMC
ΔABC cân tại A
mà AMlà trung tuyến
nên AM vuông góc BC
b: Xét ΔAHD và ΔAHE có
AD=AE
góc DAH=góc EAH
AH chung
=>ΔAHD=ΔAHE
Xét ΔABC có AD/AB=AE/AC
nên DE//BC
c: Xét ΔIEK và ΔICM có
góc IEK=góc ICM
IE=IC
góc EIK=góc CIM
=>ΔIEK=ΔICM
=>EK=MC
mà EK//MC
nên EKCM là hình bình hành
=>CK//EM

a: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED

a: Xét tứ giác EFBC có
A là trung điểm của EB
A là trung điểm của CF
Do đó: EFBC là hình bình hành
Suy ra: EF=BC

1. Xét tam giác ABD và tam giác AED có:
\(\text{+}\) AD chung.
\(\text{+}\) \(\widehat{BAD}=\widehat{EAD}\) (AD là phân giác).
\(\text{+}\) AB = AE (gt).
\(\Rightarrow\) Tam giác ABD = Tam giác AED (c - g - c).
2. a) Tam giác ABD = Tam giác AED (cmt).
\(\Rightarrow\) \(\widehat{ABD}=\widehat{AED}\) (2 góc tương ứng).
Mà \(\widehat{ABD}+\widehat{KBD}=\)\(180^o.\)
\(\widehat{AED}+\widehat{CED}=\)\(180^o.\)
\(\Rightarrow\) \(\widehat{KBD}=\widehat{CED} (đpcm).\)
b) Xét tam giác KBD và tam giác CED có:
\(\text{+}\) \(\widehat{KBD}=\widehat{CED} \) (cmt).
\(\text{+}\) BD = ED (Tam giác ABD = Tam giác AED).
\(\text{+}\) \(\widehat{BDK}=\widehat{EDC}\) (2 góc đối đỉnh).
\(\Rightarrow\) Tam giác KBD = Tam giác CED (g - c - g).
3. Ta có: KE = KD + DE; CB = CD + DB.
Mà KD = CD (Tam giác KBD = Tam giác CED).
DE = DB (Tam giác ABD = Tam giác AED).
\(\Rightarrow\) KE = CB.
Xét tam giác KBE và tam giác CEB có:
\(\text{+}\) KE = CB (cmt).
\(\text{+}\) BK = EC (Tam giác KBD = Tam giác CED).
\(\text{+}\) BE chung.
\(\Rightarrow\) Tam giác KBE = Tam giác CEB (c - c - c).
4. Ta có: DE \(\perp\) AC (gt). => Tam giác AED vuông tại E.
Mà tam giác ABD = tam giác AED (cmt).
\(\Rightarrow\) Tam giác ABD vuông tại B.
\(\Rightarrow\) \(\widehat{ABD}\) \(=90^o.\)
\(\Rightarrow\) Tam giác ABC vuông tại B.
Vậy để DE \(\perp\) AC thì tam giác ABC vuông tại B.

 Vẽ hình ghi gt và kl giúp em luôn nha
Vẽ hình ghi gt và kl giúp em luôn nha Mng giúp mình bài 1, 2, 3, 4 nha(vẽ hình luôn). Cảm ơn nhiều 🤩
Mng giúp mình bài 1, 2, 3, 4 nha(vẽ hình luôn). Cảm ơn nhiều 🤩



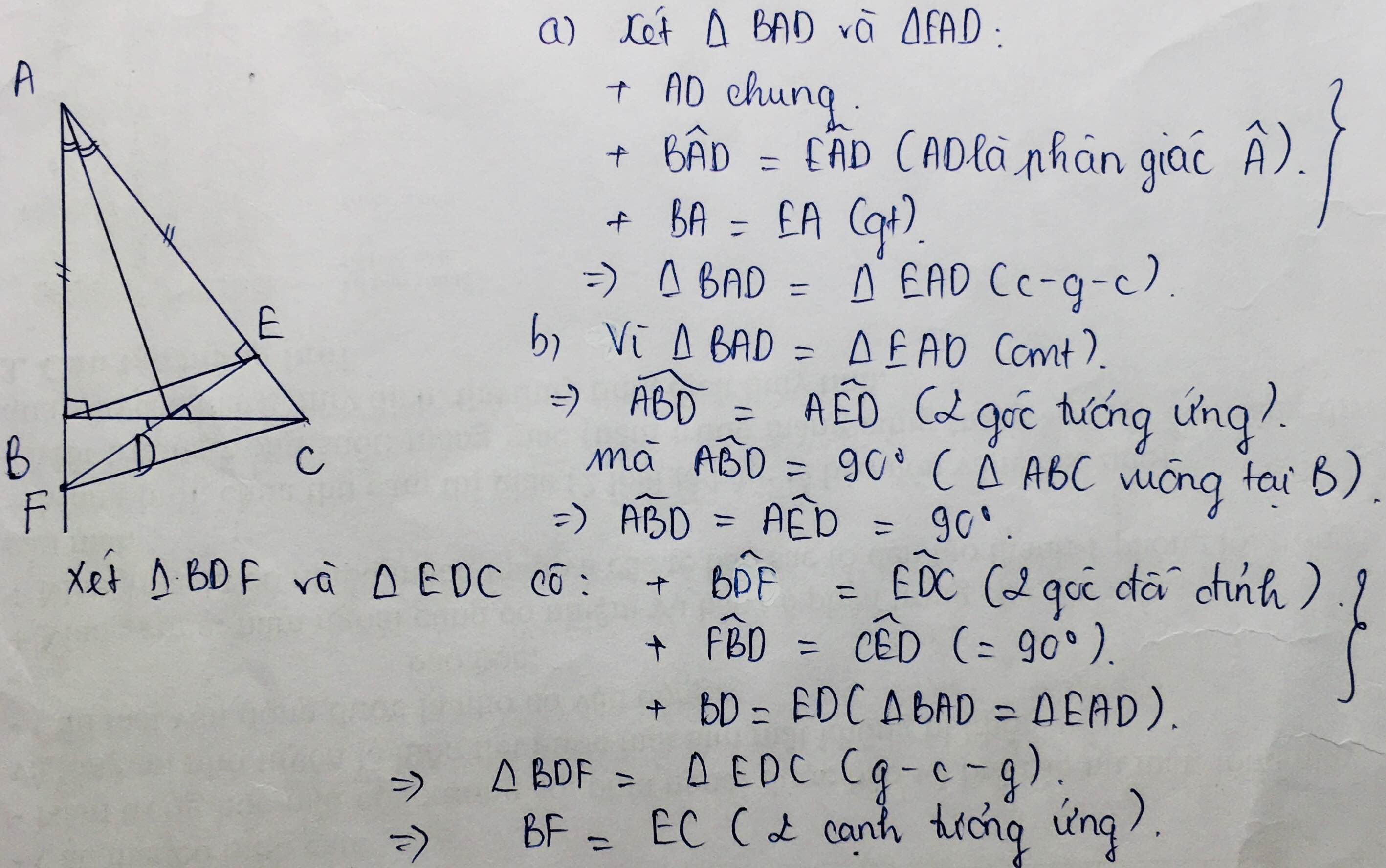



Bài 1:
a: Xét ΔAMB và ΔAMC có
AM chung
AB=AC
BM=CM
Do đó: ΔABM=ΔACM