Giải giúp mình bài 15 với ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DN
0
H
26 tháng 12 2022
\(\dfrac{9^{15}.8^{11}}{3^{29}.16^8}=\dfrac{\left(3^2\right)^{15}.\left(2^3\right)^{11}}{3^{29}.\left(2^4\right)^8}=\dfrac{3^{30}.2^{33}}{3^{29}.2^{32}}\)
Ta lấy vễ trên chia vế dưới
\(=3.2=6\)
\(\dfrac{2^{11}.9^3}{3^5.16^2}=\dfrac{2^{11}.\left(3^2\right)^3}{3^5.\left(2^4\right)^2}=\dfrac{2^{11}.3^6}{3^5.2^8}\)
Ta lấy vế trên chia vế dưới
\(=2^3.3=24\)
S
26 tháng 12 2022
\(\dfrac{9^{15}.8^{11}}{3^{29}.16^8}=\dfrac{\left(3^2\right)^{15}.\left(2^3\right)^{11}}{3^{29}.\left(2^4\right)^8}=\dfrac{3^{30}.2^{33}}{3^{29}.3^{32}}=3.2=6\)
\(\dfrac{2^{11}.9^3}{3^5.16^2}=\dfrac{2^{11}.\left(3^2\right)^3}{3^5.\left(2^4\right)^2}=\dfrac{2^{11}.3^6}{3^5.2^8}=2^3.3=8.3=24\)
TP
Thảo Phương
CTVVIP
26 tháng 7 2021
a) Gọi x, y lần lượt là số mol Al, Fe
2Al + 3H2SO4 → Al2(SO4)3 + 3H2
Fe + H2SO4 → FeSO4+ H2
\(\left\{{}\begin{matrix}27x+56y=5,54\\\dfrac{3}{2}x+y=\dfrac{3,584}{22,4}\end{matrix}\right.\)
=> x=0,06 , y =0,07
=> \(m_{Al}=1,62\left(g\right);m_{Fe}=3,92\left(g\right)\)
b) \(n_{H_2SO_4\left(pứ\right)}=n_{H_2}=0,16\left(mol\right)\)
=> \(m_{H_2SO_4\left(pứ\right)}=0,16.98=15,68\left(g\right)\)
c) \(m_{ddH_2SO_4}=\dfrac{15,68}{20\%}=78,4\left(g\right)\)
c) 2NaOH + H2SO4 → Na2SO4 + 2H2O
\(n_{H_2SO_4\left(dư\right)}=\dfrac{1}{2}n_{NaOH}=\dfrac{1}{2}.0,25.0,6=0,075\left(mol\right)\)
=> \(m_{H_2SO_4\left(bđ\right)}=15,68+0,075.98=23,03\left(g\right)\)
TD
1
AT
7 tháng 7 2021
\(\sqrt{15+5\sqrt{5}}-\sqrt{3-\sqrt{5}}=\sqrt{5}\sqrt{3+\sqrt{5}}-\sqrt{\dfrac{6-2\sqrt{5}}{2}}\)
\(=\sqrt{5}\sqrt{\dfrac{6+2\sqrt{5}}{2}}-\sqrt{\dfrac{\left(\sqrt{5}-1\right)^2}{2}}=\sqrt{5}\sqrt{\dfrac{\left(\sqrt{5}+1\right)^2}{2}}-\dfrac{\left|\sqrt{5}-1\right|}{\sqrt{2}}\)
\(=\sqrt{5}.\dfrac{\left|\sqrt{5}+1\right|}{\sqrt{2}}-\dfrac{\sqrt{5}-1}{\sqrt{2}}=\sqrt{5}.\dfrac{\sqrt{5}+1}{\sqrt{2}}-\dfrac{\sqrt{5}-1}{\sqrt{2}}\)
\(=\dfrac{5+\sqrt{5}-\sqrt{5}+1}{\sqrt{2}}=\dfrac{6}{\sqrt{2}}=3\sqrt{2}\)
HN
1
12 tháng 9 2021
\(\left(5\sqrt{3}+3\sqrt{5}\right):\sqrt{15}=\dfrac{5\sqrt{3}}{\sqrt{15}}+\dfrac{3\sqrt{5}}{\sqrt{15}}=\dfrac{5\sqrt{3}}{\sqrt{5}.\sqrt{3}}+\dfrac{3\sqrt{5}}{\sqrt{3}.\sqrt{5}}=\sqrt{5}+\sqrt{3}\)
HK
3
31 tháng 10 2021
Bạn ơi, làm như vậy thì quá ngắn rồi ạ, với lại bạn làm thiếu mất đề bài của mình rồi
DT
13 tháng 4 2022
B16:
Biểu thức C là tích của 100 phân số nhỏ hơn 1 , trong đó các tử đều lẽ , các mẫu đều chẵn . Ta đưa ra biểu thức trung gian là một tích các phân số mà tử số các phân số đều chẵn và mẫu số các phân số đều lẽ . Thêm 1 vào tử và mẫu của mỗi phân số của A , giá trị mỗi phân số tăng lên , do đó:
ta có:
\(A< \dfrac{1}{2}.\dfrac{3}{4}.\dfrac{5}{6}.....\dfrac{199}{200}\left(1\right)\)
\(A< \dfrac{2}{3}.\dfrac{4}{5}.\dfrac{6}{7}....\dfrac{200}{201}\left(2\right)\)
Nhân (1) vs (2) theo từng vế ta được:
\(A^2< \left(\dfrac{1}{2}.\dfrac{3}{4}.\dfrac{5}{6}.....\dfrac{199}{200}\right).\left(\dfrac{2}{3}.\dfrac{4}{5}.\dfrac{6}{7}....\dfrac{200}{201}\right)\)
Vế phải của bđt trên bằng \(\dfrac{1}{201}\)
Vậy \(A^2< \dfrac{1}{201}\left(đpcm\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 4 2022
15.
\(A=\dfrac{1}{4}+\dfrac{1}{4^2}+...+\dfrac{1}{4^7}\)
\(4A=1+\dfrac{1}{4}+...+\dfrac{1}{4^6}\)
\(\Rightarrow4A-A=1-\dfrac{1}{4^7}\)
\(\Rightarrow3A=1-\dfrac{1}{4^7}\)
\(\Rightarrow A=\dfrac{1}{3}\left(1-\dfrac{1}{4^7}\right)\)
\(B=\dfrac{8}{9}.\dfrac{15}{16}...\dfrac{2499}{2500}=\dfrac{2.4}{3^2}.\dfrac{3.5}{4^2}...\dfrac{49.51}{50^2}\)
\(B=\dfrac{2.3...49}{3.4...50}.\dfrac{4.5...51}{3.4...50}=\dfrac{2}{50}.\dfrac{51}{3}=\dfrac{17}{25}\)
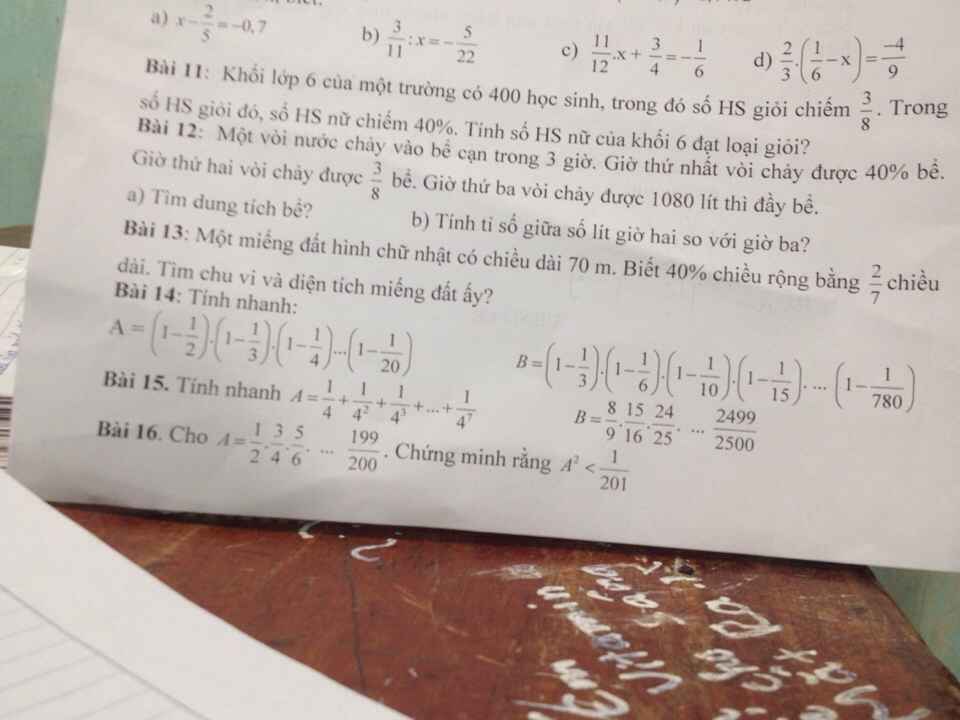
Thời gian anh Kiên đi là
120 : 50 = 2,4 giờ = 2 giờ 24 phút
Anh Kiên khởi hành lúc
10 giờ 15 phút - 2 giờ 24 phút - 20 phút = 7 giờ 31 phút