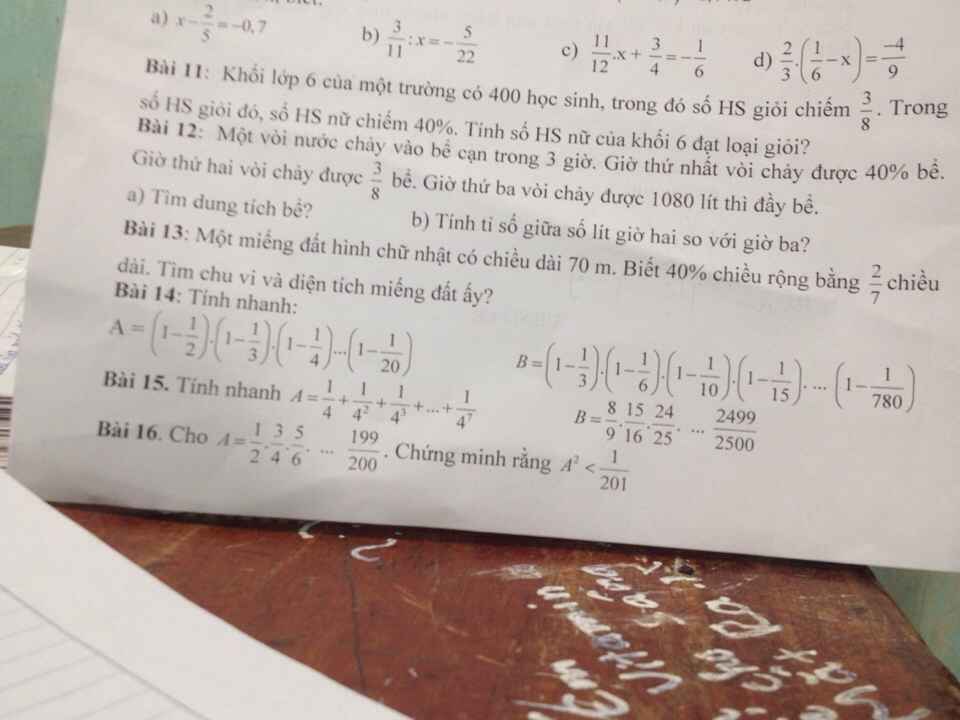
Giúp mình bài 15 với bài 16 ạ!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
H
26 tháng 12 2022
\(\dfrac{9^{15}.8^{11}}{3^{29}.16^8}=\dfrac{\left(3^2\right)^{15}.\left(2^3\right)^{11}}{3^{29}.\left(2^4\right)^8}=\dfrac{3^{30}.2^{33}}{3^{29}.2^{32}}\)
Ta lấy vễ trên chia vế dưới
\(=3.2=6\)
\(\dfrac{2^{11}.9^3}{3^5.16^2}=\dfrac{2^{11}.\left(3^2\right)^3}{3^5.\left(2^4\right)^2}=\dfrac{2^{11}.3^6}{3^5.2^8}\)
Ta lấy vế trên chia vế dưới
\(=2^3.3=24\)
S
26 tháng 12 2022
\(\dfrac{9^{15}.8^{11}}{3^{29}.16^8}=\dfrac{\left(3^2\right)^{15}.\left(2^3\right)^{11}}{3^{29}.\left(2^4\right)^8}=\dfrac{3^{30}.2^{33}}{3^{29}.3^{32}}=3.2=6\)
\(\dfrac{2^{11}.9^3}{3^5.16^2}=\dfrac{2^{11}.\left(3^2\right)^3}{3^5.\left(2^4\right)^2}=\dfrac{2^{11}.3^6}{3^5.2^8}=2^3.3=8.3=24\)
5 tháng 9 2021
Bài 16:
a: Xét ΔOEH và ΔOFH có
OE=OF
\(\widehat{EOH}=\widehat{FOH}\)
OH chung
Do đó: ΔOEH=ΔOFH
13 tháng 8 2021
Bài 16:
1) \(x^2+4x+4=\left(x+2\right)^2\)
2) \(x^2+6x+9=\left(x+3\right)^2\)
3) \(4x^2+4x+1=\left(2x+1\right)^2\)
4) \(9+12x+4x^2=\left(2x+3\right)^2\)
5) \(x^2-2x+1=\left(x-1\right)^2\)
6) \(x^2-8x+16=\left(x-4\right)^2\)
7) \(36-12x+x^2=\left(x-6\right)^2\)
8) \(4x^2-12xy+9y^2=\left(2x+3y\right)^2\)
9) \(9x^2-6x+1=\left(3x-1\right)^2\)
10) \(4x^2+12x+9=\left(2x+3\right)^2\)
11) \(x^2+3x+\dfrac{9}{4}=\left(x+\dfrac{3}{2}\right)^2\)
12) \(4x^2-6x+\dfrac{9}{4}=\left(2x-\dfrac{3}{2}\right)^2\)
13 tháng 8 2021
Bài 16:
1: \(x^2+4x+4=\left(x+2\right)^2\)
2: \(x^2+6x+9=\left(x+3\right)^2\)
3: \(4x^2+4x+1=\left(2x+1\right)^2\)
4: \(4x^2+12x+9=\left(2x+3\right)^2\)
5: \(x^2-2x+1=\left(x-1\right)^2\)
6: \(x^2-8x+16=\left(x-4\right)^2\)
7: \(36-12x+x^2=\left(6-x\right)^2\)
8: \(4x^2-12xy+9y^2=\left(2x-3y\right)^2\)
DN
0
B16:
Biểu thức C là tích của 100 phân số nhỏ hơn 1 , trong đó các tử đều lẽ , các mẫu đều chẵn . Ta đưa ra biểu thức trung gian là một tích các phân số mà tử số các phân số đều chẵn và mẫu số các phân số đều lẽ . Thêm 1 vào tử và mẫu của mỗi phân số của A , giá trị mỗi phân số tăng lên , do đó:
ta có:
\(A< \dfrac{1}{2}.\dfrac{3}{4}.\dfrac{5}{6}.....\dfrac{199}{200}\left(1\right)\)
\(A< \dfrac{2}{3}.\dfrac{4}{5}.\dfrac{6}{7}....\dfrac{200}{201}\left(2\right)\)
Nhân (1) vs (2) theo từng vế ta được:
\(A^2< \left(\dfrac{1}{2}.\dfrac{3}{4}.\dfrac{5}{6}.....\dfrac{199}{200}\right).\left(\dfrac{2}{3}.\dfrac{4}{5}.\dfrac{6}{7}....\dfrac{200}{201}\right)\)
Vế phải của bđt trên bằng \(\dfrac{1}{201}\)
Vậy \(A^2< \dfrac{1}{201}\left(đpcm\right)\)
15.
\(A=\dfrac{1}{4}+\dfrac{1}{4^2}+...+\dfrac{1}{4^7}\)
\(4A=1+\dfrac{1}{4}+...+\dfrac{1}{4^6}\)
\(\Rightarrow4A-A=1-\dfrac{1}{4^7}\)
\(\Rightarrow3A=1-\dfrac{1}{4^7}\)
\(\Rightarrow A=\dfrac{1}{3}\left(1-\dfrac{1}{4^7}\right)\)
\(B=\dfrac{8}{9}.\dfrac{15}{16}...\dfrac{2499}{2500}=\dfrac{2.4}{3^2}.\dfrac{3.5}{4^2}...\dfrac{49.51}{50^2}\)
\(B=\dfrac{2.3...49}{3.4...50}.\dfrac{4.5...51}{3.4...50}=\dfrac{2}{50}.\dfrac{51}{3}=\dfrac{17}{25}\)