(1 - x)2 + (x - x2) + 3 = 0
Giúp mình với, mình cảm ơn nhiều ạ !
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Hai bài bị trùng nhau nên các bạn nhìn ảnh hay văn bản đều như nhau ạ
c: =>x+2>0
hay x>-2
d: =>-4<=x<=3
e: =>\(x\in\varnothing\)
f: \(\Leftrightarrow\left[{}\begin{matrix}x>4\\x< -6\end{matrix}\right.\)

1.
Đặt \(x-2=t\ne0\Rightarrow x=t+2\)
\(B=\dfrac{4\left(t+2\right)^2-6\left(t+2\right)+1}{t^2}=\dfrac{4t^2+10t+5}{t^2}=\dfrac{5}{t^2}+\dfrac{2}{t}+4=5\left(\dfrac{1}{t}+\dfrac{1}{5}\right)^2+\dfrac{19}{5}\ge\dfrac{19}{5}\)
\(B_{min}=\dfrac{19}{5}\) khi \(t=-5\) hay \(x=-3\)
2.
Đặt \(x-1=t\ne0\Rightarrow x=t+1\)
\(C=\dfrac{\left(t+1\right)^2+4\left(t+1\right)-14}{t^2}=\dfrac{t^2+6t-9}{t^2}=-\dfrac{9}{t^2}+\dfrac{6}{t}+1=-\left(\dfrac{3}{t}-1\right)^2+2\le2\)
\(C_{max}=2\) khi \(t=3\) hay \(x=4\)


\(a)\left(x-2\right)\left(x^2+2x-3\right)\ge0.\)
Đặt \(f\left(x\right)=\left(x-2\right)\left(x^2+2x-3\right).\)
Ta có: \(x-2=0.\Leftrightarrow x=2.\\ x^2+2x-3=0.\Leftrightarrow\left[{}\begin{matrix}x=1.\\x=-3.\end{matrix}\right.\)
Bảng xét dấu:
x \(-\infty\) -3 1 2 \(+\infty\)
\(x-2\) - | - | - 0 +
\(x^2+2x-3\) + 0 - 0 + | +
\(f\left(x\right)\) - 0 + 0 - 0 +
Vậy \(f\left(x\right)\ge0.\Leftrightarrow x\in\left[-3;1\right]\cup[2;+\infty).\)
\(b)\dfrac{x^2-9}{-x+5}< 0.\)
Đặt \(g\left(x\right)=\dfrac{x^2-9}{-x+5}.\)
Ta có: \(x^2-9=0.\Leftrightarrow\left[{}\begin{matrix}x=3.\\x=-3.\end{matrix}\right.\)
\(-x+5=0.\Leftrightarrow x=5.\)
Bảng xét dấu:
x \(-\infty\) -3 3 5 \(+\infty\)
\(x^2-9\) + 0 - 0 + | +
\(-x+5\) + | + | + 0 -
\(g\left(x\right)\) + 0 - 0 + || -
Vậy \(g\left(x\right)< 0.\Leftrightarrow x\in\left(-3;3\right)\cup\left(5;+\infty\right).\)

Ta có: \(\left(x-1\right)^{2020}\ge0\forall x\)
\(\left|y-3\right|\ge0\forall y\)
Do đó: \(\left(x-1\right)^{2020}+\left|y-3\right|\ge0\forall x,y\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x-1=0\\y-3=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=3\end{matrix}\right.\)
Vậy: (x,y)=(1;3)

ĐKXĐ: \(x\notin\left\{1;-1\right\}\)
Ta có: \(\dfrac{x-3}{x+1}=\dfrac{x^2}{x^2-1}\)
\(\Leftrightarrow\dfrac{\left(x-3\right)\left(x-1\right)}{\left(x+1\right)\left(x-1\right)}=\dfrac{x^2}{\left(x-1\right)\left(x+1\right)}\)
Suy ra: \(x^2-4x+3-x^2=0\)
\(\Leftrightarrow-4x=-3\)
hay \(x=\dfrac{3}{4}\)(thỏa ĐK)
Vậy: \(S=\left\{\dfrac{3}{4}\right\}\)

2:
a: =>x-1=0 hoặc 3x+1=0
=>x=1 hoặc x=-1/3
b: =>x-5=0 hoặc 7-x=0
=>x=5 hoặc x=7
c: =>\(\left[{}\begin{matrix}x-1=0\\x+5=0\\3x-8=0\end{matrix}\right.\Leftrightarrow x\in\left\{1;-5;\dfrac{8}{3}\right\}\)
d: =>x=0 hoặc x^2-1=0
=>\(x\in\left\{0;1;-1\right\}\)
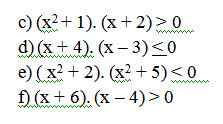 Giúp mình với, mình cần gấp ạ
Giúp mình với, mình cần gấp ạ
Ta có: \(\left(1-x\right)^2+\left(x-x^2\right)+3=0\)
\(\Leftrightarrow x^2-2x+1+x-x^2+3=0\)
\(\Leftrightarrow4-x=0\)
hay x=4
Vậy: S={4}
$⇔x^2-2x+1+x-x^2+3=0$
$⇔-x=-4$
$⇔x=4$
Vậy phương trình đã cho có tập nghiệm S={4}