Tính giá trị biểu thức: \(M=\frac{a-b}{a+b}\) với b>a>0 và 2a2+2b2=5ab
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(2a^2+2b^2=5ab\\ \Leftrightarrow2a^2-5ab+2b^2=0\\ \Leftrightarrow2a^2-4ab-ab+2b^2=0\\ \Leftrightarrow2a\left(a-2b\right)+b\left(a-2b\right)=0\\ \Leftrightarrow\left(2a+b\right)\left(a-2b\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}a=-\dfrac{b}{2}\\a=2b\end{matrix}\right.\)
Với \(a=-\dfrac{b}{2}\Leftrightarrow Q=\dfrac{-\dfrac{b}{2}+b}{-\dfrac{b}{2}-b}=\dfrac{b}{2}:\dfrac{-3b}{2}=\dfrac{b}{-3b}=-\dfrac{1}{3}\)
Với \(a=2b\Leftrightarrow Q=\dfrac{3b}{b}=3\)

\(2a^2+2b^2=5ab\)
<=>\(2a^2-5ab+2b^2=0\)
<=>\(2\left(a^2-\frac{5}{2}ab+b^2\right)=0\) <=> \(a^2-\frac{5}{2}ab+b^2=0\)
<=>\(a^2-2.a.\frac{5}{4}.b+b^2=0\)
<=>\(\left(a-\frac{5}{4}b\right)^2=0\) <=> \(a-\frac{5}{4}b=0\) <=> \(a=\frac{5}{4}b\)
Ta có: \(M=\frac{a+b}{a-b}=\frac{\frac{5}{4}b+b}{\frac{5}{4}b-b}=\frac{\left(\frac{5}{4}+1\right).b}{\left(\frac{5}{4}-1\right).b}=\frac{\frac{9}{4}b}{\frac{1}{4}b}=\frac{\frac{9}{4}}{\frac{1}{4}}=9\)
Vậy M=9

\(M=a^2-a\left|a\right|-\dfrac{b}{2}\cdot2\left|b\right|-b^2\\ M=a^2+a^2-b^2-b^2\\ M=2\left(a^2-b^2\right)\\ D\)


ĐKXĐ : \(a\ne b\)\(;\)\(a\ne-b\)
\(4a^2+b^2=5ab\)
\(\Leftrightarrow\)\(\left(4a^2-4ab\right)-\left(ab-b^2\right)=0\)
\(\Leftrightarrow\)\(4a\left(a-b\right)-b\left(a-b\right)=0\)
\(\Leftrightarrow\)\(\left(a-b\right)\left(4a-b\right)=0\)
\(\Leftrightarrow\)\(\orbr{\begin{cases}a-b=0\\4a-b=0\end{cases}\Leftrightarrow\orbr{\begin{cases}a=b\left(loai\right)\\4a=b\end{cases}}}\)
\(\Rightarrow\)\(4a=b\)
\(\Rightarrow\)\(M=\frac{ab}{a^2-b^2}=\frac{a.4a}{\left(a-b\right)\left(a+b\right)}=\frac{4a^2}{\left(a-4a\right)\left(a+4a\right)}=\frac{4a^2}{-15a^2}=\frac{-4}{15}\)
...

Ta có: \(2a^2+2b^2=5ab\Leftrightarrow2\left(a^2+2ab+b^2\right)=9ab\Leftrightarrow\left(a+b\right)^2=\frac{9ab}{2}\)
Mặt khác: \(2a^2+2b^2=5ab\Leftrightarrow2\left(a^2-2ab+b^2\right)=ab\Leftrightarrow\left(a-b\right)^2=\frac{ab}{2}\)
Do đó: \(\frac{\left(a+b\right)^2}{\left(a-b\right)^2}=\left(\frac{a+b}{a-b}\right)^2=\frac{\frac{9ab}{2}}{\frac{ab}{2}}=9\Leftrightarrow M=\frac{a+b}{a-b}=\pm3\)
Mà a > b > 0 => M = 3
Ta có: \(2a^2+2b^2=5ab\Leftrightarrow2\left(a^2+2ab+b^2\right)=9ab\Leftrightarrow\left(a+b\right)^2=\frac{9ab}{2}\)
Mặt khác: \(2a^2+2b^2=5ab\Leftrightarrow2\left(a^2-2ab+b^2\right)=ab\Leftrightarrow\left(a-b\right)^2=\frac{ab}{2}\)
Do đó: \(\frac{\left(a+b\right)^2}{\left(a-b\right)^2}=\left(\frac{a+b}{a-b}\right)^2=\frac{\frac{9ab}{2}}{\frac{ab}{2}}=9\Leftrightarrow M=\frac{a+b}{a-b}=\pm3\)
Mà \(a>b>0\Rightarrow M=3\)

\(Từ\) \(giả\) \(thiết\) : \(4a^2+b^2=\text{5}ab\)
\(\Leftrightarrow4a^2-4ab-ab+b^2\)
\(\Leftrightarrow\left(4a-b\right)\left(a-b\right)=0\)
\(TH1:\) \(4a-b=0\) \((\) \(mẫu\) \(thuẫn\) \(với\) \(2a>b\) \()\)
\(TH2:\) \(a-b=0\)
\(\Rightarrow a=b\)
\(\Rightarrow A=\dfrac{a^2}{4a^2-a^2}\)
\(\Rightarrow A=\dfrac{1}{3}\)

Bài này theo mình nên chọn phương án phân tích ĐTTNT từ điều kiện đầu tiên!
2a² + 2b² = 5ab
<=> 2a² - 5ab + 2b² = 0
<=> 2a² - 4ab - ab + 2b² = 0
<=> 2a(a - 2b) - b(a - 2b) = 0
<=> (a - 2b)(2a - b) = 0
<=> [a = 2b
.......[ a = b/2 (Loại vì a > b)
Thay a = 2b vào biểu thức ta có:
. .2b + b . . .. 3b
------------ = ---------- = 3
. .2b - b . . . . b

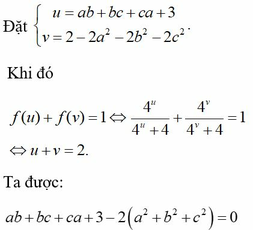
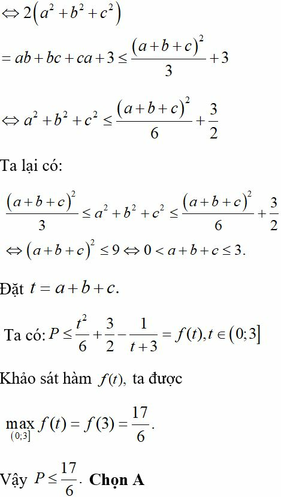
e Hoàng Phúc tui co bai tuong tu ne
M = 2(a-2ab+b) / 2(a+2ab+b) =ab/9ab = 1/9
lưu ý: a;b binh phuong nhé tui làm bieng viêt