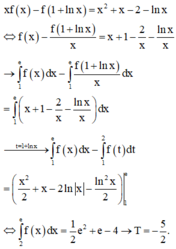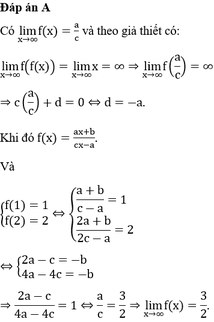Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án A
Phương pháp giải:
Hàm số đơn điệu trên đoạn nên giá trị nhỏ nhất – lớn nhất sẽ đạt tại đầu mút của đoạn
Lời giải:
Ta có 
suy ra f(x) là hàm số nghịch biến trên [a;b]
Mà 
. Vậy 
Đáp án A
Ta có 5 log c 6 = 6 log c 5 ⇔ 5 log c 6 + − 6 log c 5 = 0 . Mà
f − x = a ln 2017 x 2 + 1 − x − b x sin 2018 x + 2
a ln 2017 1 x 2 + 1 + x − b x sin 2018 x + 2 = − a ln 2017 x 2 + 1 + x − b x sin 2018 x + 2
⇒ f x + f − x = 4 ⇒ f − 6 log c 5 + f 5 log c 6 = 4 ⇒ f − 6 log c 5 = − 2
Đáp án A
Ta có 5 log c 6 = 6 log c 5 = x ⇒ − 6 log c 5 = − x
Khi đó f − x = a . ln 2017 x 2 + 1 − x − b x sin 2018 x + 2
= a . ln 2017 1 x 2 + 1 + x − b x sin 2018 x + 2
= − a . ln 2017 x 2 + 1 + b x sin 2018 x + 2 + 4
Mặt khác f x = 6 → P = f − x = − f x + 4 = − 6 + 4 = − 2
Từ giả thiết \(a+b+c=6\) ta có:
\(\left(a+b+c\right)^2=36=a^2+b^2+c^2+2\left(ab+ac+bc\right)=P+ab+ac+bc\)
Hay \(P=36-ab-bc-ca\).
Vậy GTLN của P tương đương với GTNN của \(ab+bc+ca\)
Không mất tính tổng quát giả sử \(a\) là số lớn nhất trong \(a,b,c\)
Thì \(a+b+c=6\le3a\), do đó \(4\ge a\ge2\)
Lại có: \(ab+bc+ca\ge ab+ca=a\left(b+c\right)=6\left(6-a\right)\ge8\) với \(4 \ge a \ge 2\)
Do đó GTNN của \(ab+bc+ca=8\), khi \(\left\{\begin{matrix}a=4\\b=2\\c=0\end{matrix}\right.\)
Vậy GTLN của P là \(36-8=28\) khi \(\left\{\begin{matrix}a=4\\b=2\\c=0\end{matrix}\right.\)
\(\left\{\begin{matrix}a+b+c=6\left(1\right)\\0\le a,b,c\le4\left(2\right)\end{matrix}\right.\)
Từ(1)=> \(\left\{\begin{matrix}b+c=\left(6-a\right)\\b^2+c^2+bc=\left(6-a\right)^2-bc\end{matrix}\right.\)
\(P=a^2+\left(b^2+c^2+bc\right)+a\left(b+c\right)=a^2+\left[\left(6-a\right)^2-bc\right]+a\left(6-a\right)\)
\(P=\left(a^2-12a+36\right)-bc=\left(a-6\right)^2-bc\)
Từ (2)=> \(bc\ge0\) \(\Rightarrow P\le\left(a-6\right)^2\)
đạt được khi: \(b.c=0\Rightarrow\left[\begin{matrix}b=0\\c=0\end{matrix}\right.\) (3)
từ (1)&(3) \(\Rightarrow2\le a\le4\) (4)
P lớn nhất => !a-6! lớn nhất thủa mãn (4) => a=2 Từ (1)&(3)=>\(\left[\begin{matrix}b=4\\c=4\end{matrix}\right.\)
Kết luận:
Để P(a,b,c) đạt Max trong 3 số phải có 1 số =0 (cận bé của (2) ; Một số =4 (cận lớn của (2); một số thỏa mãn điều kiện (1)
Vậy: \(P_{max}\left(a,b,c\right)=P\left(4,2,0\right)=4^2+2^2+0^2+2.4+0+0=28\)
