giải phương trình: x3 + 99x2 - 100x = 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


x3+99x2-100x=0
<=>x3+100x2-x2-100x=0
<=>x2(x+100)-x(x+100)=0
<=>(x2-x)(x+100)=0
<=>x2-x=0 (1) hoặc x+100=0 (2)
Giải (1);
x2-x=0<=>x(x-1)=0<=>x=0 hoặc x-1=0<=>x=0 hoặc x=1
Giải (2):
x+100=0=>x=-100
Vậy ....................

T a c ó 4 3 x - 5 2 - 9 9 x 2 - 25 2 = 0 4 3 x - 5 2 - 9 3 x 2 - 5 2 2 = 0 4 3 x - 5 2 - 9 3 x - 5 3 x + 5 2 = 0 4 3 x - 5 2 - 9 3 x - 5 2 3 x + 5 2 = 0 3 x - 5 2 4 - 3 3 x + 5 2 = 0 3 x - 5 2 4 - 3 3 x + 5 2 = 0 3 x - 5 2 2 2 - 9 x + 15 2 = 0 3 x - 5 2 2 + 9 x + 15 2 – 9 x – 15 = 0 3 x - 5 2 9 x + 17 - 9 x – 13 = 0
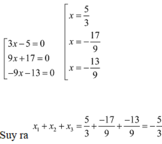
Đáp án cần chọn là: C

x + 1 2 − 1 = 0 ⇔ x + 1 2 = 1 ⇔ x + 1 = 2 ⇔ x = 1
Vậy nghiệm của phương trình là x = 1.

a) Thay m=3 vào phương trình, ta được:
\(x^2-2x+3^2-3\cdot3+5=0\)
\(\Leftrightarrow x^2-2x+5=0\)
\(\Leftrightarrow x^2-2x+1+4=0\)
\(\Leftrightarrow\left(x-1\right)^2+4=0\)(vô lý)
Vậy: Khi m=3 thì phương trình vô nghiệm

Thay `k=0` vào pt ta có:
`9x^2-25-0-0=0`
`<=>9x^2=25`
`<=>x^2=25/9`
`<=>x=+-5/3`
`b)x=-1` làm nghiệm nên ta thay `x=-1` vào pt thì pt =0
`=>9.1-25-k^2-2k(-1)=0`
`<=>-16-k^2+2k=0`
`<=>k^2-2k+16=0`
`<=>(k-1)^2+15=0` vô lý
Vậy khong có giá trị của k thỏa mãn đề bài

cosx + \(\dfrac{5}{2}\)sinx = 3
vì 12 + 2,52 < 32 nên pt vô nghiệm
\(cosx+5sin\dfrac{x}{2}-3\)=0
<=> 1-2\(sin^2\dfrac{x}{2}\)+\(5sin\dfrac{x}{2}\)-3=0
<=>2\(sin^2\dfrac{x}{2}-5sin\dfrac{x}{2}\)+2=0
<=>2si\(n^2\dfrac{x}{2}-4sin\dfrac{x}{2}-sin\dfrac{x}{2}+2\)=0
<=>(\(sin\dfrac{x}{2}-2\))(\(2sin\dfrac{x}{2}-1\))=0
\(\left[{}\begin{matrix}sin\dfrac{x}{2}=2\left(lọại\right)\\sin\dfrac{x}{2}=\dfrac{1}{2}\left(nhận\right)\end{matrix}\right.\)
vơi \(sin\dfrac{x}{2}=\dfrac{1}{2}\Leftrightarrow\left[{}\begin{matrix}\dfrac{x}{2}=\dfrac{\pi}{6}+k2\pi\\\dfrac{x}{2}=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}+k4\pi\\x=\dfrac{5\pi}{3}+k4\pi\end{matrix}\right.\)

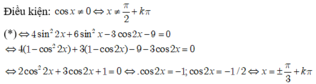
x^3-99x^2-100x
<=>x^3-x^2+100x^2-100x=0
<=>x^2(x-1)+100x(x-1)=0
<=>(x-1)(x^2+100x)=0
<=> giải tiếp ra hoặc x=1;x=0;x=-100
Bài này bấm nghiệm trên máy tính cx ra luôn mà
x^3+99x^2-100x=0
=>x(x^2+99x-100)=0
=>