1/ Cho đường tròn (O), dây AB khác đường kính. Qua O kẻ đường vuông góc với AB tại K.
a/ Chứng minh : góc AOK = góc BOK
b/ Tiếp tuyến tại M của (O) cắt OK tại C. Chứng minh: Chứng minh CN là tiếp tuyến của đường tròn (O).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
30 tháng 11 2021
Lời giải:
a. Xét tam giác $AOK$ và $BOK$ có:
$\widehat{OKA}=\widehat{OKB}=90^0$
$OK$ chung
$OA=OB=R$
$\Rightarrow \triangle AOK=\triangle BOK$ (ch-cgv)
$\Rightarrow \widehat{AOK}=\widehat{BOK}$
b. Xét tam giác $ACO$ và $BCO$ có:
$AO=BO$
$\widehat{O_1}=\widehat{O_2}$ (cm ở phần a)
$CO$ chung
$\Rightarrow \triangle ACO=\triangle BCO$ (c.g.c)
$\Rightarrow \widehat{OBC}=\widehat{OAC}=90^0$
$\Rightarrow OB\perp BC$ nên $CB$ là tiếp tuyến của $(O)$
CM
22 tháng 7 2018
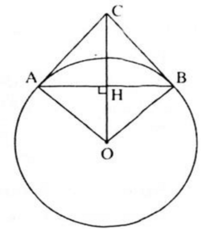
Gọi H là giao điểm của OC và AB, ΔAOB cân tại O (OA = OB, bán kính). OH là đường cao nên cũng là đường phân giác. Do đó:
Suy ra: CB vuông góc với OB, mà OB là bán kính của đường tròn (O)
⇒ CB là tiếp tuến của đường tròn (O) tại B. (điều phải chứng minh)
6 tháng 1 2023
a: ΔOAB cân tại O
mà OC là đường cao
nên OC là phân giác của góc AOB
Xét ΔOAC và ΔOBC có
OA=OB
góc AOC=góc BOC
OC chung
Do đó: ΔOAC=ΔOBC
=>góc OBC=90 độ
=>CB là tiếp tuyến của (O)
b: Xét (O) có
ΔBAD nôi tiếp
BD là đường kính
Do đó:ΔBAD vuông tại A
=>AD vuông góc với BA
=>AD//CB
5 tháng 2 2022
a: Xét (O) có
OH là một phần đường kính
AB là dây
OH⊥AB tại H
Do đó: H là trung điểm của AB
Xét ΔMAB có
MH là đường trung tuyến
MH là đường cao
Do đó:ΔMAB cân tại M
Xét ΔOAM và ΔOBM có
OA=OB
AM=BM
OM chung
Do đó:ΔOAM=ΔOBM
Suy ra: \(\widehat{OAM}=\widehat{OBM}=90^0\)
=>ΔOMB vuông tại B
=>MB là tiếp tuyến
b: Xét (O) có
ΔABC nội tiếp
BC là đường kính
Do đó:ΔABC vuông tại A
a: Xét ΔOAK vuông tại K và ΔOBK vuông tại K có
OA=OB
OK chung
Do đó: ΔOAK=ΔOBK
Suy ra: \(\widehat{AOK}=\widehat{BOK}\)