cho đường tròn (o) dây AB khác đường kính.Qua O kẻ đường vuông góc với AB tại K
a/ chúng minh góc AOK = góc BOK
b/ tiếp tuyến tại A của (o) cắt OK tại C. chứng minh: CB là tiếp tuyến của đường tròn (o)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
30 tháng 11 2021
a: Xét ΔOAK vuông tại K và ΔOBK vuông tại K có
OA=OB
OK chung
Do đó: ΔOAK=ΔOBK
Suy ra: \(\widehat{AOK}=\widehat{BOK}\)
CM
22 tháng 7 2018
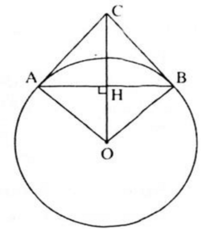
Gọi H là giao điểm của OC và AB, ΔAOB cân tại O (OA = OB, bán kính). OH là đường cao nên cũng là đường phân giác. Do đó:
Suy ra: CB vuông góc với OB, mà OB là bán kính của đường tròn (O)
⇒ CB là tiếp tuến của đường tròn (O) tại B. (điều phải chứng minh)
AH
Akai Haruma
Giáo viên
22 tháng 11 2021
Lời giải:
Gọi $T$ là giao $OC$ và $AB$
Vì $OA=OB$ nên $OAB$ là tam giác cân tại $O$
$\Rightarrow$ đường cao $OT$ đồng thời là đường trung tuyến
$\Rightarrow T$ là trung điểm $AB$
Như vậy, $OC\perp AB$ tại trung điểm $T$ của $AB$ nên $OC$ là đường trung trực của $AB$
$\Rightarrow CA=CB$.
$\triangle CBO=\triangle CAO$ (c.c.c)
$\Rightarrow \widehat{CBO}=\widehat{CAO}=90^0$
$\Rightarrow CB\perp OB$ nên $CB$ là tiếp tuyến của $(O)$ tại $C$.
NN
22 tháng 8 2021
a) Ta thấy OC là trung trực của AB nên ΔOAC = ΔOBC (c.c.c), duy ra góc OBC vuông. Do đó CB là tiếp tuyến của đường tròn.
b) AI = AB : 2 = 12 cm.
Tính được OI = 9 cm.
cm.
AT
30 tháng 7 2021
CO cắt AB tại D
Vì \(OA=OB=R\Rightarrow\Delta OAB\) cân tại O có \(OD\bot AB\Rightarrow D\) là trung điểm AB
\(\Rightarrow\) A và B đối xứng qua OC \(\Rightarrow\left\{{}\begin{matrix}\angle OAB=\angle OBA\\\angle CAB=\angle CBA\end{matrix}\right.\)
\(\Rightarrow\angle OAB+\angle CAB=\angle OBA+\angle CBA\Rightarrow\angle CAO=\angle CBO\)
\(\Rightarrow\angle CBO=90\Rightarrow CB\) là tiếp tuyến
CM
2 tháng 5 2018
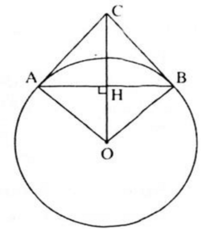
a) Gọi H là giao điểm của OC và AB, ΔAOB cân tại O (OA = OB, bán kính). OH là đường cao nên cũng là đường phân giác. Do đó:
Suy ra: CB vuông góc với OB, mà OB là bán kính của đường tròn (O)
⇒ CB là tiếp tuến của đường tròn (O) tại B. (điều phải chứng minh)
b) Ta có: OH vuông góc AB nên H là trung điểm của AB (quan hệ vuông góc giữa đường kính và dây)
Vậy OC = 25 cm
CM
27 tháng 8 2017
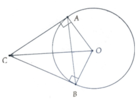
a, ∆OAC = ∆OBC (c.g.c)
=> O B C ^ - O A B ^ = 90 0
=> đpcm
b, Sử dụng hệ thức lượng trong tam giác vuông OBC tính được OC=25cm
6 tháng 1 2023
a: ΔOAB cân tại O
mà OC là đường cao
nên OC là phân giác của góc AOB
Xét ΔOAC và ΔOBC có
OA=OB
góc AOC=góc BOC
OC chung
Do đó: ΔOAC=ΔOBC
=>góc OBC=90 độ
=>CB là tiếp tuyến của (O)
b: Xét (O) có
ΔBAD nôi tiếp
BD là đường kính
Do đó:ΔBAD vuông tại A
=>AD vuông góc với BA
=>AD//CB
12 tháng 1 2023
a: \(AI=\sqrt{10^2-6^2}=8\left(cm\right)\)
AB=2*AI=16cm
b: ΔOAB cân tại O
mà OI là đường cao
nên OI là phân giác của góc AOB
Xét ΔOAM và ΔOBM có
OA=OB
góc AOM=góc BOM
OM chung
Do đó: ΔOAM=ΔOBM
=>góc OBM=90 độ
=>MB là tiêp tuyến của (O)
Lời giải:
a. Xét tam giác $AOK$ và $BOK$ có:
$\widehat{OKA}=\widehat{OKB}=90^0$
$OK$ chung
$OA=OB=R$
$\Rightarrow \triangle AOK=\triangle BOK$ (ch-cgv)
$\Rightarrow \widehat{AOK}=\widehat{BOK}$
b. Xét tam giác $ACO$ và $BCO$ có:
$AO=BO$
$\widehat{O_1}=\widehat{O_2}$ (cm ở phần a)
$CO$ chung
$\Rightarrow \triangle ACO=\triangle BCO$ (c.g.c)
$\Rightarrow \widehat{OBC}=\widehat{OAC}=90^0$
$\Rightarrow OB\perp BC$ nên $CB$ là tiếp tuyến của $(O)$
Hình vẽ:
