Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
- Tập xác định: D = R\ {1}
- Đạo hàm: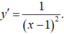 
- Đồ thị hàm số cắt trục hoành tại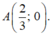 
- Hệ số góc của tiếp tuyến tại A là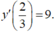 
Chọn A.
Thay tọa độ A vào ta được: \(\dfrac{b}{-1}=-1\Rightarrow b=1\)
\(\Rightarrow y=\dfrac{ax+1}{x-1}\Rightarrow y'=\dfrac{-a-1}{\left(x-1\right)^2}\)
\(y'\left(0\right)=-3\Leftrightarrow\dfrac{-a-1}{\left(0-1\right)^2}=-3\Leftrightarrow-a-1=-3\)
\(\Rightarrow a=2\)
a) Học sinh tự giải
b)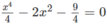 
⇔ x 4 − 8 x 2 − 9 = 0
⇔ ( x 2 + 1)( x 2 − 9) = 0
⇔ 
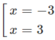
(C) cắt trục Ox tại x = -3 và x = 3
Ta có: y′ = x 3 − 4x
Phương trình tiếp tuyến của (C) tại điểm có hoành độ x = 3 và x = -3 lần lượt là:
y = y′(3)(x – 3) và y = y′(−3)(x + 3)
Hay y = 15(x – 3) và y = −15(x + 3)
c)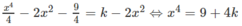 
Từ đó, ta có:
k = −9/4: (C) và (P) có một điểm chung là (0; −9/4)
k > −9/4: (C) và (P) có hai giao điểm.
k < −9/4: (C) và (P) không cắt nhau.
Đáp án C
Giao điểm của đồ thị hàm số số với trục hoành là A(-2;0).
Ta có y ' = 3 x − 1 2 ⇒ k = y ' − 2 = 1 3