Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Đồ thị hàm số đi qua điểm A(0;−1) do đó − 1 = 0 + b 0 − 1 ⇒ b = 1
Tiếp tuyến của đồ thị tại A(0;−1) có hệ số góc bằng -3, do đó y ' 0 = − 3
⇔ y ' 0 = − a − 1 0 − 1 2 = − 3 ⇔ a = 2
Vậy a+b=3.

Đáp án B
Vì đồ thị hàm số cắt trục tung tại A(0;-1) ⇒ b = 1 ⇒ y = a x + 1 x − 1
Ta có y ' = − a + 1 x − 1 2 ⇒ y ' 0 = − a − 1 = − 3 ⇔ a = 2. Vậy a = 2 , b = 1

Đáp án D
Cách giải: TXĐ: D = R
![]()
Gọi ![]() là 2 tiếp điểm
là 2 tiếp điểm
![]()
![]()
Tiếp tuyến tại M, N của (C) có hệ số góc đều bằng
![]()
![]()
![]()
![]()
Theo đề bài, ta có: OB = 2018OA => Phương trình đường thẳng MN có hệ số góc bằng 2018 hoặc – 2018.
TH1: Phương trình đường thẳng MN có hệ số góc là
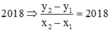
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() là nghiệm của phương trình
là nghiệm của phương trình ![]()

TH2: MN có hệ số góc là 2018. Dễ đang kiểm rằng : Không có giá trị của ![]() thỏa mãn.
thỏa mãn.
Vậy k = 6042

Phương pháp
Hệ số góc của tiếp tuyến với đồ thị hàm số y = f(x) tại điểm có hoành độ x = x 0 là k = f ' x 0 .
Cách giải
Ta có: y ' = 3 x 2 - 2
Hệ số góc của tiếp tuyến với (C) tại điểm có hoành độ x = 1 là k = 1
Chọn D.


Đáp án C
Giao điểm của đồ thị hàm số số với trục hoành là A(-2;0).
Ta có y ' = 3 x − 1 2 ⇒ k = y ' − 2 = 1 3