Tìm GTLN và GTNN của y=cos2x+cosx
K
Khách
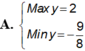
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NN
1
DD
Đoàn Đức Hà
Giáo viên
23 tháng 7 2021
\(y=\sqrt{3}cos2x+2sinxcosx-2\)
\(=\sqrt{3}cos2x+sin2x-2\)
Ta có: \(\left|\sqrt{3}cos2x+sin2x\right|\le\sqrt{\left(\sqrt{3}\right)^2+1^2}=2\)
Do đó \(-2\le\sqrt{3}cos2x+sin2x\le2\)
\(\Leftrightarrow-4\le\sqrt{3}cos2x+sin2x-2\le2\).
Ta có: \(\left|\sqrt{3}cosx-sinx\right|\le\sqrt{\left(\sqrt{3}\right)^2+\left(-1\right)^2}=2\)
Do đó \(-2\le\sqrt{3}cosx-sinx\le2\)
HP
21 tháng 8 2021
Đặt \(sinx=t\left(t\in\left[-1;1\right]\right)\)
\(y=\left|sinx+cos2x\right|=\left|2sin^2x-sinx-1\right|\)
\(\Leftrightarrow y=\left|f\left(t\right)\right|=\left|2t^2-t-1\right|\)
\(f\left(-1\right)=2\Rightarrow y=2\)
\(f\left(1\right)=0\Rightarrow y=0\)
\(f\left(\dfrac{1}{4}\right)=-\dfrac{9}{8}\Rightarrow y=\dfrac{9}{8}\)
\(\Rightarrow y_{min}=0;y_{max}=2\)
TT
0
AT
1
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 9 2021
a.
\(y=sinx.cosx+1=\dfrac{1}{2}sin2x+1\)
\(-1\le sin2x\le1\Rightarrow\dfrac{1}{2}\le y\le\dfrac{3}{2}\)
\(y_{min}=\dfrac{1}{2}\) khi \(sin2x=-1\Rightarrow x=-\dfrac{\pi}{4}+k\pi\)
\(y_{max}=\dfrac{3}{2}\) khi \(sin2x=1\Rightarrow x=\dfrac{\pi}{4}+k\pi\)
b.
\(y=2\left(\dfrac{\sqrt{3}}{2}sinx-\dfrac{1}{2}cosx\right)-2=2.sin\left(x-\dfrac{\pi}{6}\right)-2\)
\(-1\le sin\left(x-\dfrac{\pi}{6}\right)\le1\Rightarrow-4\le y\le0\)
\(y_{min}=-4\) khi \(sin\left(x-\dfrac{\pi}{6}\right)=-1\Rightarrow x=-\dfrac{\pi}{3}+k2\pi\)
\(y_{max}=0\) khi \(sin\left(x-\dfrac{\pi}{6}\right)=1\Rightarrow x=\dfrac{2\pi}{3}+k2\pi\)
Chọn A