Cho hàm số y = f x xác định và liên tục trên ℝ \ 0 thỏa mãn: x 2 f 2 x + 2 x - 1 f x = x . f ' x - 1 với đồng thời f 1 = 2 . Tính ∫ 1 4 f x d x
A. - 2 ln 2 - 1 4
B. - 2 ln 2 - 3 4
C. - ln 2 - 3 4
D. - ln 2 - 1 4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Ta có f ' x = - e x . f 2 x ⇔ f ' x f 2 x = - e x ⇔ ∫ f ' x f 2 x d x = ∫ - e x d x = ∫ d f x f 2 x d x = - e x + C
⇔ - 1 f x = - e x + C ⇔ f x = 1 e x - C mà f 0 = 1 2 ⇒ 1 1 - C = 1 2 ⇒ C = - 1
Vậy f x = 1 e x + 1 ⇒ f ln 2 = 1 e ln 2 + 1 = 1 2 + 1 = 1 3 .

Đáp án D
Ta có f ' x = - e x . f 2 x ⇔ - f ' x f 2 x = e x ⇔ ∫ - f ' x f 2 x d x = ∫ e x d x ⇔ 1 f x = e x + C
Mà f 0 = 1 2 ⇒ 1 f 0 = e 0 + C ⇔ C + 1 = 2 ⇒ C = 1 → f x = 1 e x + 1
Do đó f ' x = - e x e x + 1 2 ⇒ f ' ln 2 = - 2 9 . Vậy phương trình tiếp tuyến là 2 x + 9 y - 2 ln 2 - 3 = 0 .

Đáp án A

Ta có:
![]()
⇒ f x 5 + 4 x + 3 = 2 x + 1 ⇒ ∫ - 1 1 5 x 4 + 4 . f x 5 + 4 x + 3 d x = ∫ - 1 1 5 x 4 + 4 . ( 2 x + 1 ) d x ⇔ ∫ - 2 8 f ( t ) d t = ∫ - 1 1 ( 10 x 5 + 5 x 4 + 8 x + 4 ) d x

Chọn đáp án C.
Lấy tích phân hai vế trên đoạn [0;2] có
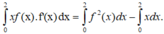
Tích phân từng phần có
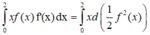
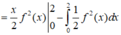
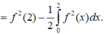
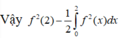
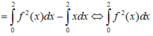
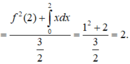
Đáp án B