Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng a, gọi φ là góc giữa hai mặt phẳng (SAB) và (CSD) Tính cos φ
A. cos φ = 1 2
B. cos φ = 1 6
C. cos φ = 1 3
D. cos φ = 1 4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A

Gọi H là trung điểm AB
![]()
nên hình chiếu của SD trên (ABCD) là HD
![]()
Tam giác SAB đều cạnh a nên SH = a 3 2
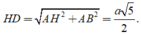
Tam giác vuông SHD
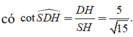

Chọn B.
+ Gọi AD = x (x > 0)
+ Kẻ![]() dễ dàng chứng minh được
dễ dàng chứng minh được ![]()
![]()
Trong tam giác SBC ta có
![]()
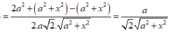
Trong tam giác SAD có ![]()
Xét tam giác AHK có
![]()
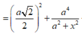
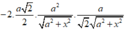
![]()
Xét tam giác AHK có
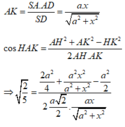
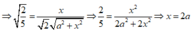
Vậy ![]()

Đáp án A.
* Hướng dẫn giải:
Dễ thấy AB = BC và A B C ⏜ = 60 o nên tam giác ABC đều.
Gọi H là hình chiếu của A lên (ABCD).
Do SA = SB =SC nên H là tâm đường tròn ngoại tiếp tam giác ABC.
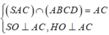
![]()
Mặt khác, H O = 1 3 B O = 1 3 . a 3 2 = a 3 6
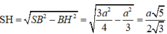
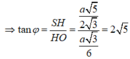
Đáp án C
Giao tuyến giữa (SAB) và (CSD) là đường thằng d qua S và song song AB, CD. Gọi I, J theo thứ tự là trung điểm AB, CD
Suy ra SI, SJ cùng vuông góc với d tại S.
Áp dụng định lý cosin trong tam giác ISJ: