Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
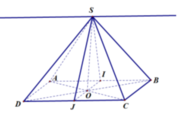
Giao tuyến giữa (SAB) và (CSD) là đường thằng d qua S và song song AB, CD. Gọi I, J theo thứ tự là trung điểm AB, CD
Suy ra SI, SJ cùng vuông góc với d tại S.
![]()
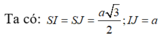
Áp dụng định lý cosin trong tam giác ISJ:
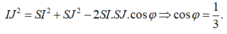

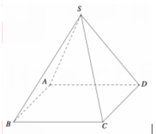
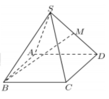
Gọi O là tâm đáy \(\Rightarrow SO\perp\left(ABCD\right)\)
\(\Rightarrow\widehat{SAO}\) hay \(\widehat{SAC}\) là góc giữa SA và (ABCD)
\(AC=\sqrt{AB^2+BC^2}=a\sqrt{2}\)
\(cos\widehat{SAC}=\dfrac{SA^2+AC^2-SC^2}{2SA.AC}=\dfrac{\sqrt{2}}{2}\)

Đáp án A
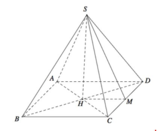
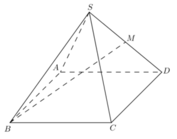
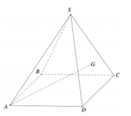
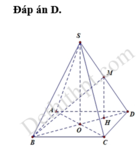
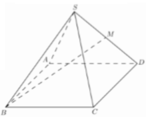
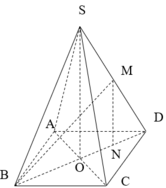
Gọi O là tâm hình vuông ABCD và M là trung điểm CD có S O = a 2 2 và H là hình chiếu vuông góc của G lên mặt phẳng (ABCD).
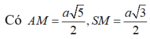
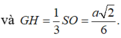
Vì
![]()
![]()
![]()
Và
![]()
![]()
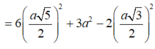
![]()
Vì vậy
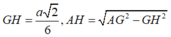
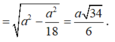
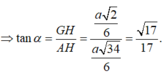
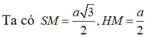
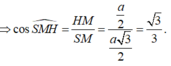
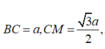
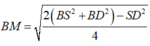
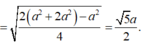
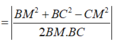
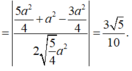



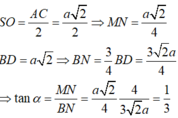



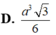

ĐÁP ÁN: B