Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D

Gọi N, K là trung điểm của BB', A'B'
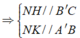
![]()
Ta tính được
![]()
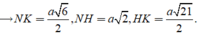
Áp dụng định lí hàm cosin ta suy ra

Cách 2. Chọn hệ trục tọa độ Oxyz với
![]()
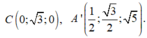
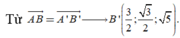

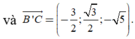
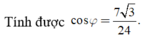

Chọn A

Gọi H là trung điểm AB
![]()
nên hình chiếu của SD trên (ABCD) là HD
![]()
Tam giác SAB đều cạnh a nên SH = a 3 2
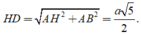
Tam giác vuông SHD
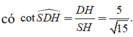

Đáp án A
Ta có: B là hình chiếu của B lên (ABCD)
A là hình chiếu của S lên (ABCD)
Suy ra góc tạo bởi (ABCD) là góc φ = S B A ^ .
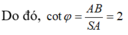

Đáp án A
Đặt a> 0 cạnh hình vuông là Dễ thấy
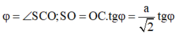
Gọi O là tâm của đáy. Vẽ AH ⊥ SC tại, H, AH cắt SO tại I thì A I O ^ = φ
![]()
Qua I vẽ đường thẳng song song DB cắt SD, SB theo thứ tự tại K, L. Thiết diện chính là tứ giác
ALHK và tứ giác này có hai đường chéo AH ⊥ KL Suy ra
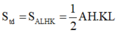
Ta có:


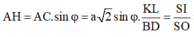
![]()
Theo giả thiết
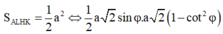
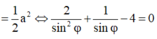
Giải được
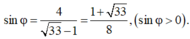
Suy ra φ = a r c sin 33 + 1 8

Chọn D.
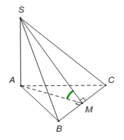
Gọi M là trung điểm của BC, suy ra AM ⊥ BC.
Ta có
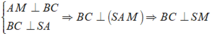
Do đó
![]()
Tam giác ABC đều cạnh a, suy ra trung tuyến AM = a 3 2
Tam giác vuông SAM, có
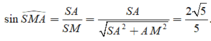

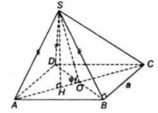
a) Tam giác ABD có AB = AD ( do ABCD là hình thoi)
=> Tam giác ABD cân tại A. Lại có góc A= 60o
=> Tam giác ABD đều.
Lại có; SA = SB = SD nên hình chóp S.ABD là hình chóp đều.
* Gọi H là tâm của tam giác ABD
=>SH ⊥ (ABD)
*Gọi O là giao điểm của AC và BD.
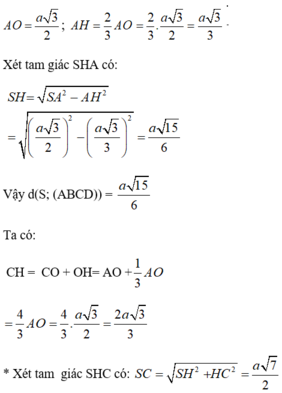


Lời giải:
Gọi $O$ là tâm đáy thì $SO\perp (ABCD)$
Ta thấy:
$BO\perp AC, BO\perp SO\Rightarrow BO\perp (AC, SO)$
Hay $BO\perp (SAC)(*)$
Gọi $T$ là trung điểm $AB$, $OH\perp ST$.
$OT\perp AB$
$SO\perp AB$
$\Rightarrow (SOT)\perp AB$
$\Rightarrow OH\perp AB$
Mà $OH\perp ST$
$\Rightarrow OH\perp (AB, ST)$ hay $OH\perp (SAB)(**)$
Từ $(*); (**)\Rightarrow \cos a=\cos \widehat{HOB}$
Trong đó:
$BO=\frac{2\sqrt{2}}{2}=\sqrt{2}$
$SO=\sqrt{SB^2-BO^2}=\sqrt{(2\sqrt{2})^2-(\sqrt{2})^2}=\sqrt{6}$
$ST=\sqrt{SO^2+OT^2}=\sqrt{6+1}=\sqrt{7}$
$OH=\frac{SO.OT}{ST}=\frac{\sqrt{6}.1}{\sqrt{7}}=\sqrt{\frac{6}{7}}$
Vì $OH\perp (SAB)$ nên tam giác $BHO$ vuông tại $H$. Do đó:
$\cos a=\cos \widehat{HOB}=\frac{HO}{OB}=\frac{\sqrt{6}}{\sqrt{7}.\sqrt{2}}=\frac{\sqrt{3}}{\sqrt{7}}$
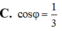
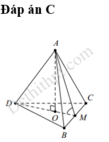

Đáp án C
Giao tuyến giữa (SAB) và (CSD) là đường thằng d qua S và song song AB, CD. Gọi I, J theo thứ tự là trung điểm AB, CD
Suy ra SI, SJ cùng vuông góc với d tại S.
Áp dụng định lý cosin trong tam giác ISJ: