Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
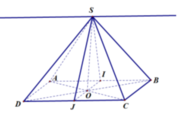
Giao tuyến giữa (SAB) và (CSD) là đường thằng d qua S và song song AB, CD. Gọi I, J theo thứ tự là trung điểm AB, CD
Suy ra SI, SJ cùng vuông góc với d tại S.
![]()
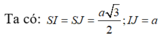
Áp dụng định lý cosin trong tam giác ISJ:
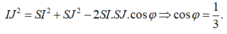

Gọi giao điểm của BO và AC là J; giao điểm của CO và AB là I.
Kẻ AK vuông góc CC’.
Vì đường thẳng CC’ vuông góc mp(ABK ) nên BK vuông góc CC’.
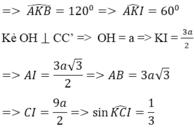
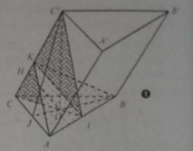
Đáp án C

Gọi D là trung điểm AB \(\Rightarrow A'D\perp\left(ABC\right)\)
\(\Rightarrow CD\) là hình chiếu vuông góc của A'C lên (ABC)
\(\Rightarrow\widehat{A'CD}\) là góc giữa A'C và (ABC) \(\Rightarrow\widehat{A'CD}=60^0\)
\(CD=\dfrac{AB\sqrt{3}}{2}=a\sqrt{3}\) (trung tuyến tam giác đều)
\(\Rightarrow A'D=CD.tan60^0=3a\)
Từ D kẻ \(DE\perp AC\) (E thuộc AC)
Mà \(A'D\perp\left(ABC\right)\Rightarrow A'D\perp AC\)
\(\Rightarrow AC\perp\left(A'DE\right)\Rightarrow\widehat{AED}\) là góc giữa (A'AC) và (ABC)
\(DE=AD.sinA=a.sin60^0=\dfrac{a\sqrt{3}}{2}\)
\(\Rightarrow A'E=\sqrt{A'D^2+DE^2}=\dfrac{a\sqrt{39}}{2}\)
\(\Rightarrow cos\widehat{A'ED}=\dfrac{DE}{A'E}=\dfrac{\sqrt{13}}{13}\)

Chọn D.
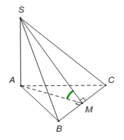
Gọi M là trung điểm của BC, suy ra AM ⊥ BC.
Ta có
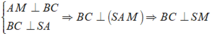
Do đó
![]()
Tam giác ABC đều cạnh a, suy ra trung tuyến AM = a 3 2
Tam giác vuông SAM, có
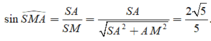

Đáp án A
Ta có: B là hình chiếu của B lên (ABCD)
A là hình chiếu của S lên (ABCD)
Suy ra góc tạo bởi (ABCD) là góc φ = S B A ^ .
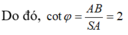

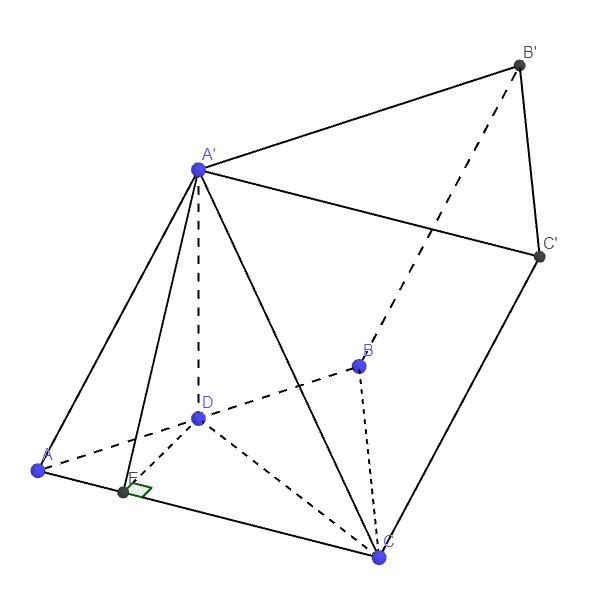
Qua A kẻ đường thẳng song song CI cắt BC kéo dài tại D
\(\Rightarrow CI||\left(A'AD\right)\Rightarrow d\left(A'A;CI\right)=d\left(CI;\left(A'AD\right)\right)=d\left(H;\left(A'AD\right)\right)\)
Từ H kẻ \(HE\perp AD\), từ H kẻ \(HF\perp A'E\)
\(\Rightarrow HF\perp\left(A'AD\right)\Rightarrow HF=d\left(H;\left(A'AD\right)\right)\)
Tứ giác AIHE là hình chữ nhật (3 góc vuông) \(\Rightarrow HE=AI=\dfrac{a}{2}\)
\(A'H\perp\left(ABC\right)\Rightarrow\widehat{A'AH}\) là góc giữa \(A'A\) là (ABC)
\(\Rightarrow\widehat{A'AH}=45^0\)
\(CI=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều) \(\Rightarrow IH=\dfrac{1}{2}CI=\dfrac{a\sqrt{3}}{4}\)
\(\Rightarrow AH=\sqrt{AI^2+IH^2}=\dfrac{a\sqrt{7}}{4}\)
\(\Rightarrow A'H=AH.tan45^0=\dfrac{a\sqrt{7}}{4}\)
Hệ thức lượng:
\(HF=\dfrac{HE.A'H}{\sqrt{HE^2+A'H^2}}=\dfrac{a\sqrt{77}}{22}\)
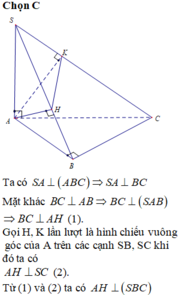

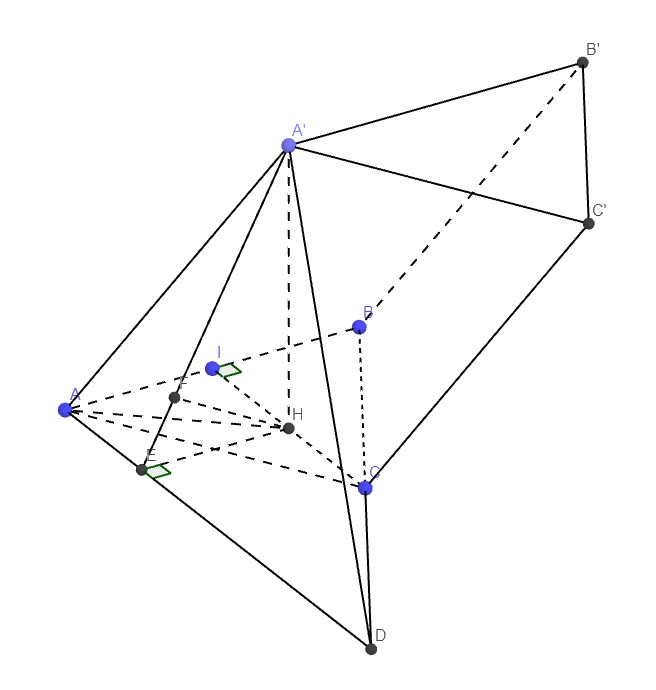
Chọn D
Gọi N, K là trung điểm của BB', A'B'
Ta tính được
Áp dụng định lí hàm cosin ta suy ra
Cách 2. Chọn hệ trục tọa độ Oxyz với