Cho a + b + c = 0. Tính C = a b a 2 + b 2 - c 2 + b c b 2 + c 2 - a 2 + c a c 2 + a 2 - b 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
9 tháng 1 2018
Đúng(0)
Những câu hỏi liên quan
PT
3
DN
0
MH
25 tháng 4 2023
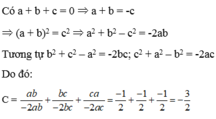
Ta có: \(a+b+c=0\Rightarrow a^2=\left(b+c\right)^2\Rightarrow a^2-2bc=b^2+c^2\)
\(\Rightarrow a^2-b^2-c^2=a^2-a^2+2bc=2bc\)
Tương tự: \(b^2-c^2-a^2=2ca;c^2-a^2-b^2=2ab\)
\(A=\dfrac{a^2}{2bc}+\dfrac{b^2}{2ca}+\dfrac{c^2}{2ab}=\dfrac{a^3+b^3+c^3}{2abc}\)
Lại có: \(a+b+c=0\Rightarrow-a=b+c\)
\(\Rightarrow-a^3=b^3+c^3+3bc\left(b+c\right)\)
\(\Rightarrow a^3+b^3+c^3=-3bc\left(b+c\right)=3abc\left(b+c=-a\right)\)
=> \(A=\dfrac{3abc}{2abc}=\dfrac{3}{2}\)
1 tháng 2 2016
\(a+b+c=0\Rightarrow-a=b+c\Rightarrow a^2=b^2+c^2+2bc\Rightarrow b^2+c^2=a^2-2bc\)
Tương tự như vậy ta được: \(a^2+c^2=b^2-2ac;a^2+b^2=c^2-2ab\)
Suy ra: \(B=\frac{a^2}{a^2-b^2-c^2}+\frac{b^2}{b^2-c^2-a^2}+\frac{c^2}{c^2-b^2-a^2}\)
\(=\frac{a^2}{a^2-\left(a^2-2bc\right)}+\frac{b^2}{b^2-\left(b^2-2ac\right)}+\frac{c^2}{c^2-\left(c^2-2ab\right)}\)
\(=\frac{a^2}{2bc}+\frac{b^2}{2ac}+\frac{c^2}{2ab}=\frac{a^3+b^3+c^3}{2abc}=\frac{\left(a+b+c\right)^3-3\left(a+b\right)\left(b+c\right)\left(c+a\right)}{2abc}\)
Ta lại thấy a+b=-c;b+c=-a;c+a=-b (a+b+c=0)
Vậy \(B=\frac{0^3-3.\left(-c\right)\left(-a\right)\left(-b\right)}{2abc}=\frac{3abc}{2abc}=\frac{3}{2}\)
NL
2
12 tháng 3 2016
a+b+c=0 suy ra a+b=-c ; a+c=-b ; b+c=-a
bình phương hết lên ta có
a^2+b^2+2ab=c^2 ; a^2+c^2+2ac=b^2 ; b^2+c^2+2bc=a^2
suy ra a^2+b^2-c^2=-2ab ; a^2+c^2-b^2=-2ac ; b^2+c^2-a^2=-2bc
thay vào B=-1/2(1/ab+1/bc+1/ac)=-1/2(c/abc+a/abc+b/abc)=0 do abc khác 0 và a+b+c=0
NT
19 tháng 12 2016
http://diendantoanhoc.net/topic/152549-t%C3%ADnh-fraca2a2-b2-c2-fracb2b2-c2-a2fracc2c2-b2-a2/
5 tháng 12 2019
Ta có \(a+b+c=0\)
=> \(a=-b-c\)
=> \(a^2=\left(b+c\right)^2\)
=> \(a^2-b^2-c^2=\left(b+c\right)^2-b^2-c^2\)
\(=b^2+2bc+c^2-b^2-c^2\) \(=2bc\)
Tương tự : \(b^2-c^2-a^2=2ac\)
\(c^2-a^2-b^2=2ab\)
Thay vào A, ta có:
\(A=\frac{a^2}{2ab}+\frac{b^2}{2ac}+\frac{c^2}{2ab}=\frac{a^3+b^3+c^3}{2ab}\)
Ta chứng minh được \(a^3+b^3+c^3-3abc=\left(a+b+c\right)\left(a^2+b^2+c^2-ac-ab-bc\right)\)
mà \(a+b+c=0\) => \(a^3+b^3+c^3-3abc=0\) => \(a^3+b^3+c^3=3abc\)
Lại thay vào A:
\(A=\frac{3abc}{2abc}=\frac{3}{2}\)
Vậy \(A=\frac{3}{2}\)
5 tháng 12 2019
Cách chứng minh \(a^3+b^3+c^3-3abc=\left(a+b+c\right)\left(a^2+b^2+c^2-ac-bc-ab\right)\)
Ta có \(a^3+b^3+c^3-3abc=\left(a^3+b^3\right)+c^3-3abc\)
\(=\left(a+b\right)^3-3ab\left(a+b\right)+c^3-3abc\)
= \(\left[\left(a+b\right)^3+c^3\right]-\left[3ab\left(a+b\right)-3abc\right]\)
\(=\left(a+b+c\right)\left[\left(a+b\right)^2-c\left(a+b\right)+c^2\right]-3ab\left(a+b+c\right)\)
\(=\left(a+b+c\right)\left(a^2+2ab+b^2-ca-bc+c^2-3ab\right)\)
\(=\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ca\right)\)
