
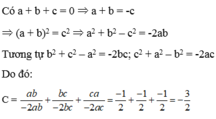
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

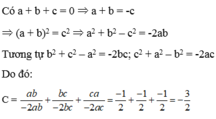


http://diendantoanhoc.net/topic/152549-t%C3%ADnh-fraca2a2-b2-c2-fracb2b2-c2-a2fracc2c2-b2-a2/


a+b+c=0 suy ra a+b=-c ; a+c=-b ; b+c=-a
bình phương hết lên ta có
a^2+b^2+2ab=c^2 ; a^2+c^2+2ac=b^2 ; b^2+c^2+2bc=a^2
suy ra a^2+b^2-c^2=-2ab ; a^2+c^2-b^2=-2ac ; b^2+c^2-a^2=-2bc
thay vào B=-1/2(1/ab+1/bc+1/ac)=-1/2(c/abc+a/abc+b/abc)=0 do abc khác 0 và a+b+c=0

1. Ta có : \(\left(\frac{1}{a}-\frac{1}{b}\right)^2\ge0\Rightarrow\frac{1}{a^2}+\frac{1}{b^2}\ge\frac{2}{ab}\)
Tương tự : \(\frac{1}{b^2}+\frac{1}{c^2}\ge\frac{2}{bc}\); \(\frac{1}{a^2}+\frac{1}{c^2}\ge\frac{2}{ac}\)
\(\Rightarrow\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\ge\frac{1}{ab}+\frac{1}{bc}+\frac{1}{ac}\). Dấu " = " xảy ra \(\Leftrightarrow\)a = b = c
\(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=3\Rightarrow\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}+2\left(\frac{1}{ab}+\frac{1}{bc}+\frac{1}{ac}\right)=9\)
\(9\le3\left(\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\right)\)\(\Rightarrow\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\ge3\)
Dấu " = " xảy ra \(\Leftrightarrow\)a = b = c = 1
\(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=7\)\(\Rightarrow\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}+2\left(\frac{1}{ab}+\frac{1}{bc}+\frac{1}{ac}\right)=49\)
\(\Rightarrow\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}+2.\frac{a+b+c}{abc}=49\)
\(\Rightarrow\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}=49\)

Ta có :
\(a+b+c=0\Rightarrow b+c=-a\Rightarrow\left(b+c\right)^2=\left(-a\right)^2\)
\(\Rightarrow b^2+2bc+c^2=a^2\Rightarrow a^2-b^2-c^2=2bc\)
Tương tự \(b^2-c^2-a^2=2ca;c^2-a^2-b^2=2ab\)
Mặt khác \(\left(b+c\right)^2=\left(-a\right)^2\Rightarrow b^3+3bc\left(b+c\right)+c^3=-a^3\Rightarrow a^3+b^3+c^3=-3bc\left(b+c\right)\)
\(\Rightarrow a^3+b^3+c^3=3abc\)
\(\Rightarrow P=\frac{a^2}{a^2-b^2-c^2}+\frac{b^2}{b^2-c^2-a^2}+\frac{c^2}{c^2-a^2-b^2}=\frac{a^2}{2bc}+\frac{b^2}{2ac}+\frac{c^2}{2ba}=\frac{a^3+b^3+c^3}{2abc}\)
\(=\frac{3abc}{2abc}=\frac{3}{2}\)
Vậy P = 3/2

\(a+b=c\Rightarrow\left(a+b\right)^2=c^2\Rightarrow a^2+2ab+b^2=c^2\Rightarrow a^2+b^2-c^2=-2ab\)
Tượng tự: \(b^2+c^2-a^2=2bc,c^2+a^2-b^2=2ac\)
Khi đó: \(B=\frac{-1}{2ab}+\frac{1}{2bc}+\frac{1}{2ac}=\frac{-c+a+b}{2abc}=0\)
Chúc bạn học tốt.