Tính diện tích của hình phẳng giới hạn bởi các đường sau: y = 2 x 2 + x – 6 và 2y = - x 2 + 3x + 6
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn B.
Phương trình hoành độ giao điểm của hai đồ thị hàm số y = x3 + 3x và y = -x là: x3 + 4x = 0 ⇔ x = 0
Ta có: x3 + 4x ≤ 0, ∀ x ∈ [-2;0].
Do đó:
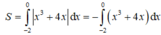
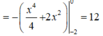

Chọn B.
Đặt h x = x 3 + 11 x - 6 - 6 x 2 = x 3 - 6 x 2 + 11 x - 6 h x = 0 ⇔ x = 1 ∨ x = 2 ∨ x = 3 ( l o ạ i )
Bảng xét dấu
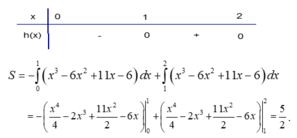

Đáp án A
Phương trình hoành độ giao điểm e x = 2 ⇔ x = ln 2
Suy ra diện tích cần tìm bằng S = ∫ 0 ln 2 e x - 2 d x + ∫ ln 2 0 e x - 2 d x = 4 ln 2 + e - 5 .

Miền cần tính diện tích được thể hiện trên Hình 10:
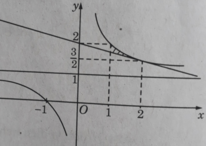
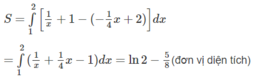
(vì tiếp tuyến với đồ thị của 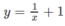
tại điểm (2;3/2) có phương trình là
![]()

Phương trình hoành độ giao điểm của hai đường y = x và x - 2 y = 0 ⇔ y = x 2 là x = x 2 ⇔ x ≥ 0 x = x 2 4 ⇔ x = 0 hoặc x = 4
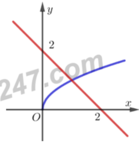
Diện tích hình phẳng cần tìm là
S ∫ 0 4 x - x 2 d x = ∫ 0 4 x - x 2 d x = 2 x 3 3 - x 2 4 0 4 = 4 3
Diện tích toàn phần của một khối tứ diện đều cạnh 2 3 4 3 là S x q = 4 . 2 3 4 3 2 3 4 = 4 3
Đáp án D

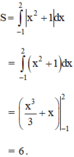
Miền cần tính diện tích được thể hiện bởi Hình 9 (học sinh tự làm)
Như vậy, với mọi x ∈ (-2;3) đồ thị của hàm số
nằm phía trên đồ thị của hàm số
Vậy ta có: