K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 3 2023
\(\left(x+1\right)e^x=0\Rightarrow x=-1\)
\(S=\int\limits^0_{-2}\left|\left(x+1\right)e^x\right|dx=-\int\limits^{-1}_{-2}\left(x+1\right)e^xdx+\int\limits^0_{-1}\left(x+1\right)e^xdx\)
\(=\dfrac{2e-2}{e^2}\)
1 tháng 4 2017
a) Diện tích hình phẳng cần tìm là:
S=2∫−1(x2+1)dx=(x33+x)∣∣2−1=6
b) Diện tích hình phẳng cần tìm là:
S=e∫1e| lnx |dx=e∫1e|lnx|dx+e∫1|lnx|dx=−1∫1elnxdx+e∫1lnxdxS=∫1ee|lnx|dx=∫1ee|lnx|dx+∫1e|lnx|dx=−∫1e1lnxdx+∫1elnxdx
Mặt khác:
∫lnxdx=xlnx−∫xdlnx=xlnx−∫dx=xlnx−x+C∫lnxdx=xlnx−∫xdlnx=xlnx−∫dx=xlnx−x+C
Do đó:
S=−1∫1elnxdx+e∫1lnxdx=1e∫1lnxdx+e∫1xdx=(xlnx−x)∣∣∣1e1+(xlnx−x)∣∣e1=2(1- \(\dfrac{1}{e}\))
Khó quá, làm mà điên não
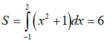
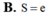
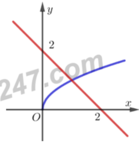
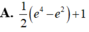
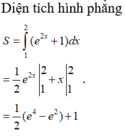
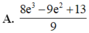
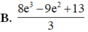
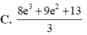
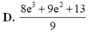
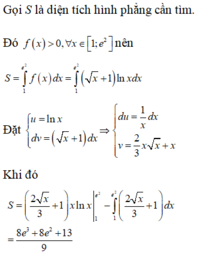
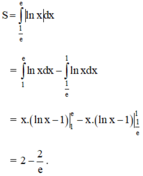
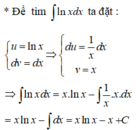
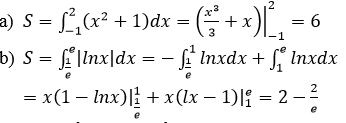
Diện tích cần tính là: