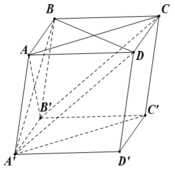
Cho hình hộp ABCD.A'B'C'D' có tất cả các cạnh đều bằng 1 và các góc phẳng đỉnh A đều bằng 60 o . Tính khoảng cách giữa hai đường thẳng AB' và A' C'
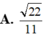
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


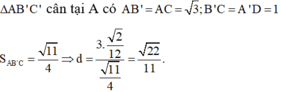

Đáp án A
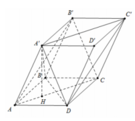
Do các góc phẳng đỉnh A đều bằng 60 ∘ và
nên các tam giác A ’ A D ; A ’ A B ; A B D là các tam giác đều cạnh 1.
Ta có:
A ' C ' / / A C ⇒ d A B ' ; A ' C ' = d A B ' C ; A ' C ' = d C ' ; A B ' C = 3 V C ' . A B ' C S . A B ' C
Mặt khác A ’ . A B D là hình tứ diện đều cạnh 1.
Ta có A H = 2 3 . A O = 3 3 ⇒ A ' H = A A ' 2 − A H 2 = 6 3 .
V = S A B C D = V A . C C ' B ' = 1 2 V A . C C ' B ' B = V 6 = 2 12
Δ A B ' C ' cân tại A có A B ' = A C = 3 ; B ' C = A ' D = 1
S A B ' C = 11 4 ⇒ d = 3. 2 12 11 4 = 22 11 .

Đáp án A.
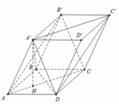
Ta có AA'BC là chóp đều có tất cả các cạnh bằng 1
![]()
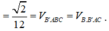
Ta có ![]()
![]()
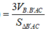
Lại có
∆
AB'C có B'C = A'D = 1; ![]() (do là hình thoi cạnh 1 có
B
A
D
^
=
60
0
)
(do là hình thoi cạnh 1 có
B
A
D
^
=
60
0
)
Do đó
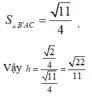

Đáp án C
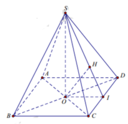
Vì A B / / C D nên d A B ; S C = d A B ; S C D
= d A ; S C D = 2 d O ; S C D = 2 O H , trong đó I là trung điểm của CD và H là hình chiếu vuông góc của O xuống SI.
Ta có: O I = a 2 ; S I = a 2 − a 2 2 = a 3 2 ; S O = a 3 2 2 − a 2 2 = a 2 2
1 O H 2 = 1 O S 2 + 1 O I 2 = 1 a 2 2 2 + 1 a 2 2 = 6 a 2 ⇒ O H = a 6
⇒ d A B ; S C = 2. a 6 = a 6 3