Một người khối lượng m = 50kg đứng trên thuyền khối lượng m 1 = 150 k g . Người này dùng dây nhẹ kéo thuyền thứ 2 khối lượng 250kg về phía mình. Lúc đầu 2 thuyền nằm yên trên mặt nước và cách nhau s = 9m. Lực kéo ngang không đổi là F = 30N.Lực cản của nước vào mỗi thuyền là 10N. Gia tốc của 2 thuyền có độ lớn:
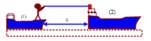
A. a 1 = 0 , 1 m / s 2 ; a 2 = 0 , 05 m / s 2
B. a 1 = 0 , 15 m / s 2 ; a 2 = 0 , 08 m / s 2
C. a 1 = 0 , 2 m / s 2 ; a 2 = 0 , 1 m / s 2
D. a 1 = 0 , 1 m / s 2 ; a 2 = 0 , 08 m / s 2

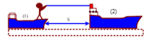
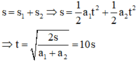

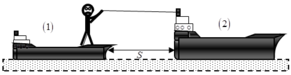
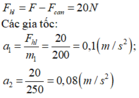
Chọn đáp án D
? Lời giải:
+ Hợp lực tác dụng vào mỗi thuyền: