Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Vận tốc của hệ hai vật sau khi va chạm
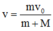
= 0,4 m/s
Quá trình va chạm không làm thay đổi vị trí cân bằng của hệ
→ v = v m a x
→ Biên độ dao động mới
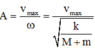
= 5cm

Đáp án B
Ban đầu hai vật cùng dao động với A = 8 ( c m ) và ω = k 2 m
Khi tới vị trí cân bằng chúng có v 0 = ω A thì chúng rời nhau; tiếp đó:
+ m 1 dao động với tốc độ cực đại vẫn là ω A nhưng với: ω ' = k m = ω 2 do đó A ' = A 2
+ m 2 chuyển động thẳng đều với vận tốc v 0 và sau thời gian t = T ' 4 = 1 4 . 2 π ω ' = π 2 ω 2 đi được s = v 0 t = A π 2 2
Vậy m 2 cách vị trí lúc đầu: s + A = 8 π 2 2 + 8 ≈ 16,9 ( c m )

Đáp án D
Theo định lý động năng ta có W d 2 − W d 1 = A ⇔ 0 , 5 m v 2 − 0 = F s ⇒ v = 5 2 m / s

Chọn đáp án A
Áp dụng định luật bảo toàn động lượng: m v = ( m + 2 m ) V ⇒ V = v 3
Chú ý: Va cham ở bài toán trên là va chạm mềm

Đáp án C
Phân tích lực tác dụng lên vật lực đàn hồi F đ hướng lên, phản lực N hướng lên, trọng lực P hướng xuống. ĐL II Newton cho vật: P - N - F đ = ma
Khi vật rời giá đỡ 
Tại vị trí cân bằng
F
đ
= P 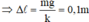
Vật cách vị trí cân băng 1 đoạn: 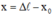 = 0,01m
= 0,01m
Quãng đường vật đi được tới khi rời giá là s = 9 - 1 = 8cm = 0,08m
Vận tốc của vật khi rời giá ![]() = 0,4m/s
= 0,4m/s
Biên độ dao động của vật là: 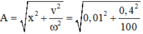 = 0,041m =4,12cm
= 0,041m =4,12cm



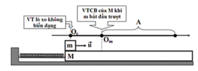
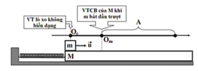


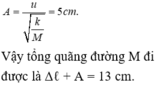

Ban đầu động lượng của hệ thuyền+ người bằng 0
Khi người đi từ mũi đến lái thì động lượng của người bằng \(\overrightarrow{p_1}=m\overrightarrow{v_1}\) ( với \(\overrightarrow{v_1}\) là vận tốc của người đối với bờ sông), còn thuyền sẽ có động lượng \(\overrightarrow{p_2}=M\overrightarrow{v_2}\) với \(\overrightarrow{v_2}\) là vận tốc của thuyền đối với bờ.
Theo phương ngang hệ không chịu tác dụng của ngoại lực ( do bỏ qua ma sát) nên động lượng của hệ được bảo toàn: \(\overrightarrow{0}=\overrightarrow{p_1}+\overrightarrow{p_2}=m\overrightarrow{v_1}+M\overrightarrow{v_2}\)
Suy ra: \(\overrightarrow{v_2}=-\frac{m}{M}m\overrightarrow{v_1}\left(1\right)\)
thuyền chuyển động ngược chiều với người.
Chọn chiều dương là chiều chuyển động của người và kí hiệu \(\overrightarrow{v_0}\) là vận tốc của người so với thuyền.
Áp dụng công thức cộng vận tốc ta có:
\(\overrightarrow{v_1}=\overrightarrow{v_0}+\overrightarrow{v_2}\leftrightarrow v_1=v_0-v_2\left(2\right)\)
Kí hiệu \(1\) là chiều dài của thuyền và \(t\) là thời gian người đi từ mũi đến lái.
Ta có: \(v_0=\frac{1}{t};v_2=\frac{s}{t},s\) là đoạn đường thuyền đi được trong thời gian \(t\)
Từ đó : \(v_1=v_0-v_2=\frac{1-s}{t}\)
Theo \(\left(1\right)\): \(mv_1=Mv_2\)
Suy ra: \(m\frac{1-s}{t}=M\frac{s}{t}\leftrightarrow s=\frac{ml}{m+M}=1m\)
Khi người đi từ mũi đến lái thì động lượng của người bằng , với
, với  là vận tốc của người đối với bờ sông, còn thuyề sẽ có động lượng
là vận tốc của người đối với bờ sông, còn thuyề sẽ có động lượng  , với
, với  là vận tốc của thuyền đối với bờ.
là vận tốc của thuyền đối với bờ.
 là vận tốc người so với thuyền.
là vận tốc người so với thuyền.
 ,
, , s là đoạn đường thuyền dịch chuyển trong thời gian t.
, s là đoạn đường thuyền dịch chuyển trong thời gian t. .mà
.mà  .từ đó ta được
.từ đó ta được 
áp dụng định luật bảo toàn động lượng ta suy ra:
dấu trừ cho thấy thuyền chuyển động ngược chiều với người.
chọn chiều dương là chiều chuyển động của người và kí hiệu
Áp dụng công thức cộng vận tốc và chiếu ta được:
ta có
từ đó: