Cho parabol ( P ) : y = 1 2 x 2 và đường tròn (C) có bán kính bằng 1 tiếp xúc với trục hoành đồng thời có chung một điểm A duy nhất với (P). Diện tích hình phẳng giới hạn bởi (P), (C) và trục hoành(phần bôi đậm trong hình vẽ) bằng
A. 3 3 + 2 - π 3
B. 29 3 - 9 π 24
C. 9 3 + 9 - 4 π 12
D. 27 3 - 8 π 24

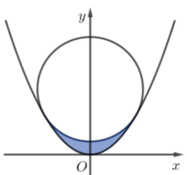
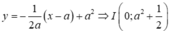

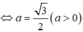
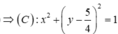
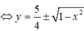

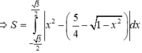
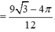

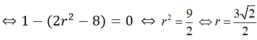
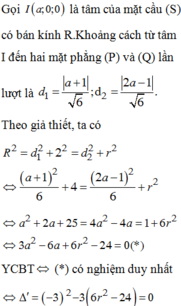
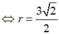
Ta cần tìm phương trình của đường tròn:
Vì đường tròn có bán kính bằng 1 và tiếp xúc với trục hoành nên tâm của đường tròn là I(t;1), (t > 0) phương trình của đường tròn là x - 1 2 + y - 1 2 = 1 .
Theo giả thiết đường tròn (C) có chung một điểm AA duy nhất với (P). nên tiếp tuyến tA tại A của (P) cũng là tiếp tuyến của (C).
Xét điểm A a ; 1 2 ; a 2 ,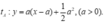
Ta có hệ điều kiện:
A ∈ ( C ) I A ⊥ t A
Vậy phương trình đường tròn
Diện tích hình phẳng cần tính là
Chọn đáp án D.