Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do tâm (C) thuộc \(\Delta\) nên có dạng: \(I\left(-2a-3;a\right)\)
\(d\left(I;d\right)=R\Leftrightarrow\dfrac{\left|-2a-3-a+1\right|}{\sqrt{1^2+\left(-1\right)^2}}=\sqrt{2}\)
\(\Leftrightarrow\left|3a+2\right|=2\Rightarrow\left[{}\begin{matrix}a=0\\a=-\dfrac{4}{3}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}I\left(-3;0\right)\\I\left(-\dfrac{1}{3};-\dfrac{4}{3}\right)\end{matrix}\right.\)
Có 2 đường tròn thỏa mãn: \(\left[{}\begin{matrix}\left(x+3\right)^2+y^2=2\\\left(x+\dfrac{1}{3}\right)^2+\left(y+\dfrac{4}{3}\right)^2=2\end{matrix}\right.\)

Do tâm nằm trên đường thẳng ∆: x + 2y – 6 = 0 nên tâm là I(6 – 2y; y).
Đường tròn tiếp xúc với hai trục tọa độ nên:
6 − 2 y = y ⇔ 6 − 2 y = y 6 − 2 y = − y ⇔ − 3 y = − 6 − y = − 6 ⇔ y = 2 y = 6
Bán kính đường tròn là R = 2 hoặc R = 6
ĐÁP ÁN B

Giả sử đường tròn cần lập có tâm O; bán kính R.
Đường thẳng Δ đi qua M(2; -2) và có VTPT là n→(4; 3) nên đường thẳng này có 1 VTCP là u→(3; -4) . Phương trình tham số của đường thẳng Δ là:
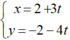
O nằm trên Δ ⇒ O(2 + 3t; -2 – 4t)
Đường tròn (O; R) tiếp xúc với d1 và d2 ⇒ d(O; d1) = d(O; d2) = R
Ta có: d(O; d1) = d(O; d2)
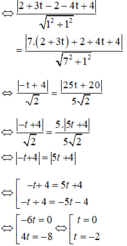
+ Với t = 0 ⇒ O(2; -2) ⇒ R = d(O; d1) = 2√2
Phương trình đường tròn: (x – 2)2 + (y + 2)2 = 8.
+ Với t = -2 ⇒ O(-4; 6) , R = d(O; d1) = 3√2
Phương trình đường tròn: (x + 4)2 + (y – 6)2 = 18
Vậy có hai phương trình đường tròn thỏa mãn là:
(x – 2)2 + (y + 2)2 = 8 hoặc (x + 4)2 + (y – 6)2 = 18

Do tâm nằm trên đường thẳng ∆: x + 2y – 5 = 0 nên tâm I(5 – 2y; y). Mà đường tròn tiếp xúc với hai đường thẳng d 1 : 3 x − y + 5 = 0 v à d 2 : x + 3 y − 13 = 0 nên có bán kính R = d I ; d 1 = d I ; d 2
⇒ 3 ( 5 − 2 y ) − y + 5 3 2 + ( − 1 ) 2 = 5 − 2 y + 3 y − 13 1 2 + 3 2
⇒ 20 − 7 y 10 = − 8 + y 10 ⇔ 20 − 7 y = − 8 + y ⇔ 400 − 280 y + 49 y 2 = 64 − 16 y + y 2 ⇔ 48 y 2 − 264 y + 336 = 0 ⇔ y = 2 y = 7 2
Tương ứng ta có hai bán kính của (C) là R 1 = 6 10 , R 2 = 9 2 10
Đáp án là D.


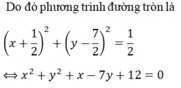
Tâm I thuộc đường thẳng x+y-3=0 nên I(a;3-a).
Đường tròn có tâm I bán kính R=1 tiếp xúc với trục hoành nên
d(I,Ox)=|3-a|=1, suy ra 3-a=1 hoặc 3-a=-1