Cho tứ diện OABC có ba cạnh OA, OB và OC đôi một vuông góc. Gọi H là chân đường vuông góc hạ từ O tới mặt phẳng (ABC). Chứng minh rằng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
23 tháng 2 2018
Chọn D
Từ giả thiết suy ra: ΔABC cân tại A có:
Gọi I là trung điểm của BC ⇒ A I ⊥ B C
Giả sử H là trực tâm của tam giác ABC.
Ta thấy O A ⊥ O B C
Vì O B ⊥ O A C ⇒ O B ⊥ A C và A C ⊥ B H nên A C ⊥ O B H ⇒ O H ⊥ A C ( 1 )
B C ⊥ O A I ⇒ O H ⊥ B C ( 2 )
Từ (1) và (2) suy ra O H ⊥ A B C
Có O I = 1 2 B C = a 2 2 = O A
=> ΔAOI vuông cân tại O => H là trung điểm AI và O H = 1 2 A I = a 2
Khi đó:
CM
1 tháng 11 2018
Đáp án D
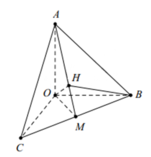
Gọi M là trung điểm của B C ⇒ B M ⊥ O A M
Vì O H ⊥ A B C ⇒ 1 O H 2 = 1 O A 2 + 1 O B 2 + 1 O C 2 ⇒ O H = a 2
Tam giác OAH vuông tại H, có A H = O A 2 − O H 2 = a 2
Diện tích tam giác vuông OAH là S Δ O A H = 1 2 . O H . A H = a 2 8
Thể tích khối chóp OABH là
V O A B H = 1 3 . B M . S Δ O A H = 1 3 . a 2 2 . a 2 8 = a 3 2 48
CM
3 tháng 10 2018
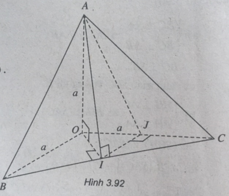
a) (BC ⊥ OA & BC ⊥ OI ⇒ BC ⊥ (OAI)
⇒ (ABC) ⊥ (OAI).
b) + Xác định góc α giữa AB và mặt phẳng (AOI)
(A ∈ (OAI) & BI ⊥ (OAI) ⇒ ∠[(AB,(OAI))] = ∠(BAI) = α.
+ Tính α:
Trong tam giác vuông BAI, ta có: sinα = 1/2 ⇒ α = 30o.
c) Xác định góc β giữa hai đường thẳng AI và OB:
Gọi J là trung điểm OC,
ta có: IJ // OB và IJ ⊥ (AOC). Như vậy:
∠[(AB,OB)] = ∠[(AI,IJ)] = ∠(AIJ) = β.
+ Tính góc:
Trong tam giác IJA,
ta có: tan β = AJ/IJ = √5 ⇒ β = arctan√5.
a) Ta có:
Do H là chân đường vuông góc hạ từ O tới mặt phẳng (ABC) nên:
OH ⊥ (ABC) ⇒ OH ⊥ BC (2)
Mà OA; OH ⊂ (OAH); OA ∩ OH = O (3)
Từ (1); (2) và (3) ⇒ BC ⊥ (OAH)
⇒ BC ⊥ AH
Chứng minh tương tự ta có: AC ⊥ BH
⇒ H là trực tâm ΔABC.
b) Gọi M = AH ∩ BC.
+ BC ⊥ (OAH) ⇒ BC ⊥ OM.
ΔOBC vuông tại O có đường cao OM
+ OA ⊥ (OBC) ⇒ OA ⊥ OM ⇒ ΔOAM vuông tại O.
OH ⊥ (ABC) ⇒ OH ⊥ AM.