Cho nửa đường tròn đường kính AB và dây MN có độ dài bằng bán kính (M thuộc cung AN, M khác A, N khác B). Các tia AM và BN cắt nhau tại I, các dây AN và BM cắt nhau tại K.
a. Chứng minh rằng: IK vuông góc với AB
b. Chứng minh rằng:AK.AN+BK.BM=AB2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
29 tháng 9 2017
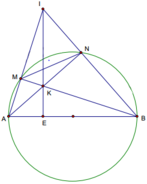
Chỉ ra sđ MN=60o nên tính được AIB=60o , do đó điểm I thuộc cung chứa góc 60o dựng trên đoạn AB.
Diện tích tam giác IAB lớn nhất khi IE lớn nhất (IE là đường cao của tam giác IAB), khi đó I nằm chính giữa cung chứa góc 60o dựng trên đoạn AB tương ứng với MN song song với AB.
7 tháng 12 2021
ta có góc CBM là góc nội tiếp chắn cung CM
góc MBA là góc nội tiếp chắn cung MA
mà cung CM= cung MA( vì M là điểm chính giữa của cung CA)
=> góc CBM= góc MBA
hay BM là tia phân giác của góc CBA
CM tương tự ta có: AN là tia phân giác của góc CAB
xét tam giác CAB có
2 tia phân giác BM và AN cắt nhau tại I
=> I là tâm đường tròn nội tiếp tam giác CAB
=> CI là tia phân giác của góc ACB(đpcm)
a. Ta thấy AN^ BI ,BM ^AI , nên K là trực tâm tam giác IAB. Do đó IK^ AB
b. Vì DAEK∽ DANB ∽ nên AK. AN =AE .AB
Tương tự vì DBEK∽ DBMA ∽ nên BK .BM =BE. BA
Vậy AK.AN+BK.BM=AE.AB+BE.BA=AB2