Cho ΔABC đồng dạng với ΔA'B'C'theo hệ tỉ số k1=4, ΔABC đồng dạng với ΔA''B''C'' theo hệ số tỉ lệ k2=1/3. Hỏi ΔA'B'C' đông dạng với ΔA''B''C'' theo hệ tỉ số nào ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
19 tháng 8 2017
ΔA'B'C' 
ΔA''B''C'' theo tỉ số đồng dạng k1 ⇒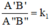 
ΔA''B''C''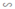 
ΔABC theo tỉ số đồng dạng k2 ⇒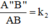 
Mà ΔA'B'C'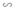 
ΔA''B''C''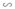; ΔA''B''C'' 
ΔABC
⇒ ΔA'B'C'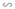 
ΔABC (theo tính chất 3)
Tỉ số đồng dạng:
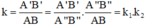
Vậy tam giác A'B'C' đồng dạng với tam giác ABC theo tỉ số k1.k2.
AH
Akai Haruma
Giáo viên
15 tháng 3 2021
Lời giải:
Giả sử $AB=3, AC=4, BC=5$ (cm)
Vì $3^2+4^2=5^2$ nên theo định lý Pitago đảo thì $ABC$ là tam giác vuông tại $A$
$A'B'C'$ đồng dạng với $ABC$ nên $A'B'C'$ là tam giác vuông tại $A'$
$\Rightarrow S_{A'B'C'}=\frac{A'B'.A'C'}{2}=54\Rightarrow A'B'.A'C'=108(*)$ (cm)
$ABC\sim A'B'C'\Rightarrow \frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{C'A'}{CA}$
$\Leftrightarrow \frac{A'B'}{3}=\frac{B'C'}{5}=\frac{C'A'}{4}(**)$
Từ $(*); (**)$ suy ra $A'B'=9; B'C'=15; C'A'=12$ (cm)
24 tháng 2 2022
e làm a,b chung luôn nha chị
Xét tam giác ABC và tam giác A`B`C`, có:
\(\dfrac{AB}{A`B`}=\dfrac{BC}{B`C`}=2\) ( gt )
Góc A = góc A` = 90 độ
=> tam giác ABC đồng dạng tam giác A`B`C`
=>\(\dfrac{AC}{A`C`}=\dfrac{AB}{A`B`}=\dfrac{BC}{B`C`}=2\) ( tính chất 2 tam giác đồng dạng )
8 tháng 4 2022
ta có : ΔABC~ΔDEF (gt)
=>\(\dfrac{AB}{DE}=\dfrac{AC}{DF}=\dfrac{BC}{\text{EF}}=k\)
=> DE = 3:2= 1,5 (cm)
DF = 4:2 = 2 (cm)
BC = 5:2 = 2,5 (cm )
=> Chu vi tam giác DEF = DE+DF+BC = 1,5+2+2,5 = 6(CM)
8 tháng 4 2022
Ta có:
\(\dfrac{AB}{DE}=2;\dfrac{AC}{DF}=2;\dfrac{BC}{EF}=2\)
\(\Leftrightarrow\dfrac{3}{DE}=2;\dfrac{4}{DF}=2;\dfrac{5}{EF}=2\)
\(\Leftrightarrow DE=\dfrac{3}{2};DF=\dfrac{4}{2};EF=\dfrac{5}{2}\)
\(\Rightarrow C_{DEF}=\dfrac{3}{2}+\dfrac{4}{2}+\dfrac{5}{2}=\dfrac{12}{2}=6\left(cm\right)\)
CM
10 tháng 1 2019
Vì ΔABC ~ ΔDHE với tỉ số đồng dạng 2 3 nên tỉ số đồng dạng của hai tam giác DHE và ABC là 3 2 .
Vậy tỉ số hai đường cao tương ứng của ΔDHE và ΔABC là 3 2
Đáp án: B
