Question

[Lê Hoài Anh]

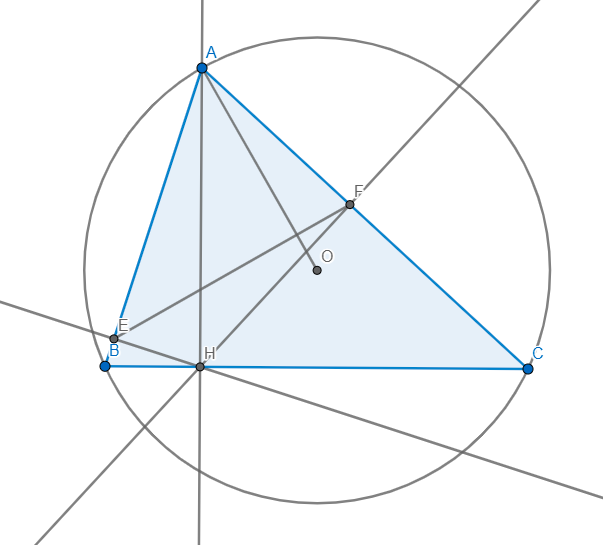
Cho đường tròn (o) ngoại tiếp tam giác nhọn ABC.Vẽ đường cao AH (H thuộc cạnh BC).Vẽ HE vuông góc với AB (E thuộc AB),HF vuông góc với AC (F thuộc AC).
a) CMR: AEHF là tứ giác nội tiếp
b) CMR: góc ABC + góc HFE = 90^o
c) Gọi M là giao điểm của BF và HE,N là giao điểm của HF và CE.
Chứng minh rằng MN song song với BC
Mình cần gấp giúp mình với!!!

Answer 1

[Ngoc Quynhh]

a) Ta có: \(HE\perp AB\) , \(HF\perp AC\) -> \(\widehat{HEA}\) + \(\widehat{HFA}=180^o\) -> \(AEHF\) nội tiếp.

b) -> \(\widehat{ABC}+\widehat{HFE}=\widehat{ABH}+\widehat{HAE}=90^o\)

c) Ta có: \(AH\perp BC\) , \(HE\perp AB\) , \(HF\perp AC\) , \(AEHF\) nội tiếp.

-> \(\widehat{AEF}=\widehat{AHF}=\widehat{ACH}\left(\widehat{HAC}=90^O\right)\) -> \(EFCB\:\) nội tiếp.

Mà ta có: \(HE\perp AB\) , \(HF\perp AC\rightarrow\widehat{MEB}=\widehat{NFC}=90^O\)

mà \(\widehat{EFB}=\widehat{EFC}\) do \(EFCB\) nội tiếp.

-> \(\widehat{EBM}=\widehat{FCN}\rightarrow\widehat{EMB}=\widehat{FNC}\)

-> \(\widehat{EMF}=\widehat{ENF}\rightarrow EFNM\) nội tiếp.

-> \(\widehat{ENM}=\widehat{EFM}=\widehat{ECB}\rightarrow MN//BC\)