Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) từ đề bài ta có:
\(HE\perp AB,HF\perp AC\Rightarrow\widehat{AEH}+\widehat{AFH}=90^O+90^O=180^O\)
\(\Rightarrow AEHF\) nội tiếp
b) từ câu a\(\rightarrow\widehat{HFE}=\widehat{HAE}=\widehat{HAB}\)
\(\Rightarrow\widehat{ABC}+\widehat{HFE}=\widehat{ABC}+\widehat{BAH}=90^O\)
c) Ta có : AEHF nội tiếp
\(\Rightarrow\widehat{AEF}=\widehat{AHF}=\widehat{ACB}\left(+\widehat{FHC}=90^O\right)\)
→EFCB nội tiếp
\(\Rightarrow\widehat{BEC}=\widehat{BFC}\)
\(\Rightarrow\widehat{BEC}-90^O=\widehat{BFC}-90^O\)
\(\Rightarrow\widehat{HEC}=\widehat{HFB}\)
→EFNM nội tiếp
\(\Rightarrow\widehat{ENM}=\widehat{EFB}=\widehat{ECB}\)
\(\Rightarrow MN//BC\)

a) \(\hept{\begin{cases}\widehat{HFE}=\widehat{HAE}\\\widehat{HAE}+\widehat{ABH}=90^O\end{cases}\Rightarrow\widehat{HFE}+\widehat{ABH}=90^O}\)
=> \(\widehat{HFE}+\widehat{ABC}=90^O\)(đpcm)
b) AEHF nội tiếp => \(\widehat{AEF}=\widehat{AHF}\)
Mà \(\widehat{AHF}=\widehat{ACB}\)( cùng phụ với \(\widehat{HAC}\))
=> \(\widehat{AEF}=\widehat{ACB}\)
=> BEFC là tứ giác nội tiếp
\(\Rightarrow\hept{\begin{cases}\widehat{EBF}=\widehat{FCE}\\\widehat{BEM}=\widehat{NFC}=90^O\end{cases}\Rightarrow\widehat{EMB}=\widehat{FNC}}\)
\(\Rightarrow\widehat{EMF}=\widehat{ENF}\)
=> EMNF là tứ giác nội tiếp
=> góc ENM = góc EFB
Mà BEFC nội tiếp => góc EFB = góc ECB
Từ 2 điều trên => góc ENM = góc ECB
=> MN // BC => đpcm

xét tam giác AEF zà tam giác ACB có
góc A chung
góc AEF= góc AHF = góc C
=> tam gác AEF ~ tam giác ACB(gg
\(\frac{AE}{AC}=\frac{AF}{AB}\)
=> tam giác AEC ~ tam giác AFB(c.g.c)
=> góc ABF = góc ACE
mà \(\hept{\begin{cases}\widehat{ABF}+\widehat{EMB}=90^0\\ACE+\widehat{CNF}=90^0\end{cases}}\)
=> góc EMB = góc CNF
lại có \(\hept{\begin{cases}\widehat{EMB}=\widehat{HMF(}đđ)\\\widehat{CNF}=\widehat{HNE}\left(dđ\right)\end{cases}}\)
=> góc HMF = góc HNE
=> tam giác HMF ~ tam giác HNE (gg)
=> \(\frac{HM}{HN}=\frac{HF}{HE}\)
=> tam giác HMN ~ tam giác HFE (gg)
=> góc HEF = góc HNM
mà góc HEF= góc HAC = góc FHC
=> góc HNM = góc FHC
=> MN//BC

a) Ta có: \(\angle AEH+\angle AFH=90+90=180\Rightarrow AEHF\) nội tiếp
b) AEHF nội tiếp \(\Rightarrow\angle EFA=\angle EHA=90-\angle BHE=\angle ABC\)
c) Ta có: \(\angle OAC=\dfrac{180-\angle AOC}{2}=90-\dfrac{1}{2}\angle AOC=90-\angle ABC\)
\(\Rightarrow\angle OAC+\angle ABC=90\Rightarrow\angle OAC+\angle AFE=90\Rightarrow OA\bot EF\)
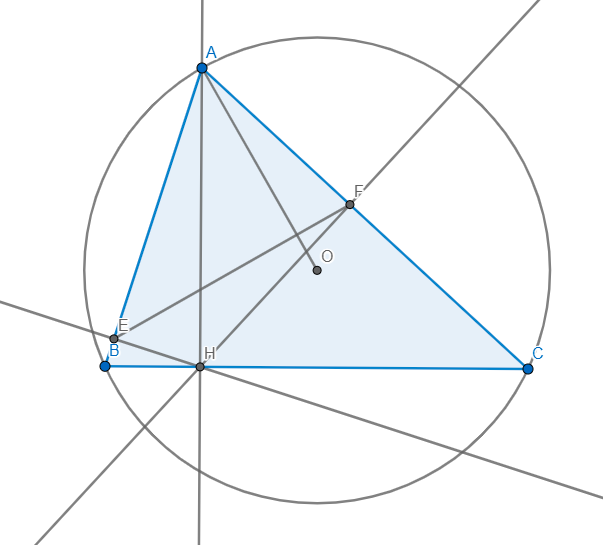
a) Ta có: \(HE\perp AB\) , \(HF\perp AC\) -> \(\widehat{HEA}\) + \(\widehat{HFA}=180^o\) -> \(AEHF\) nội tiếp.
b) -> \(\widehat{ABC}+\widehat{HFE}=\widehat{ABH}+\widehat{HAE}=90^o\)
c) Ta có: \(AH\perp BC\) , \(HE\perp AB\) , \(HF\perp AC\) , \(AEHF\) nội tiếp.
-> \(\widehat{AEF}=\widehat{AHF}=\widehat{ACH}\left(\widehat{HAC}=90^O\right)\) -> \(EFCB\:\) nội tiếp.
Mà ta có: \(HE\perp AB\) , \(HF\perp AC\rightarrow\widehat{MEB}=\widehat{NFC}=90^O\)
mà \(\widehat{EFB}=\widehat{EFC}\) do \(EFCB\) nội tiếp.
-> \(\widehat{EBM}=\widehat{FCN}\rightarrow\widehat{EMB}=\widehat{FNC}\)
-> \(\widehat{EMF}=\widehat{ENF}\rightarrow EFNM\) nội tiếp.
-> \(\widehat{ENM}=\widehat{EFM}=\widehat{ECB}\rightarrow MN//BC\)