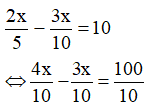Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x (km/h) là vận tốc lúc về. Điều kiện: x > 0
Ta có vận tốc lúc đi là x + 10 (km/h)
Thời gian lúc đi là 150/(x + 10) (giờ)
Thời gian lúc về là 150/x (giờ)
Thời gian nghỉ là 3 giờ 15 phút = 3.(1/4) (giờ) = 13/4 (giờ)
Theo đề bài, ta có phương trình:
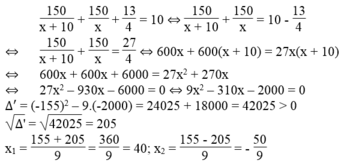
Giá trị x = - 50/9 không thỏa mãn điều kiện bài toán.
Vậy vận tốc ô tô lúc về là 40km/h.

Thời gian đi trên đường (không tính thời gian nghỉ) mà ô tô đi từ Hà Nội- Thanh Hóa và từ Thanh Hóa - Hà Nội là:
10 giờ 45 phút- 2 giờ = 8 giờ 45 pút= 8,75 giờ
+) Gọi thời gian lúc đi là x. (x>0) (giờ)
Khi đó thời gian lúc về là 8,75- x (giờ)
+) Quãng đường từ Hà Nội- Thanh Hóa lúc đi là 40x (km)
Quãng đường từ Thanh Hóa - Hà Nội lúc về là 30 (8,75-x) (km)
Vì đi và về cùng trên một quãng đường nên ta có phương trình:
\(40x=30\left(8,75-x\right)\\ < =>40x+30x=262,5\\ < =>70x=262,5\\ =>x=\dfrac{262,5}{70}=3,75\left(TMĐK\right)\)
Vậy: Quãng đường Hà Nội- Thanh Hóa dài : \(3,75.40=150\left(km\right)\)
Lời giải:
Gọi a (km) (a > 0) là quãng đường Hà Nội – Thanh Hóa.
Thời gian lúc đi là \(\frac{a}{40}\) (giờ).
Thời gian lúc về là \(\frac{a}{30}\) (giờ).
Tổng thời gian đi và về không kể thời gian nghỉ ở Thanh Hóa là:
10 giờ 45 phút – 2 giờ = 8 giờ 45 phút \(=8^3_4\) giờ \(=\frac{35}{4}\) giờ.
Theo đề bài, ta có phương trình: \(\frac{a}{40}+\frac{a}{30}=\frac{35}{4}\)
\(\Leftrightarrow\frac{3a}{120}+\frac{4a}{120}=\frac{1050}{120}\Leftrightarrow3a+4a=1050\Leftrightarrow7a=1050\Leftrightarrow a=150\) (thỏa mãn)
Vậy quãng đường Hà Nội – Thanh Hóa dài 150 km.

Gọi chiều dài quãng đường từ Hà Nội đến Thanh Hóa là x km.
Thời gian đi từ Hà Nội đến Thanh Hóa với vận tốc 40 km/h là:
t1 = x/40
Sau đó, ôtô nghỉ lại ở Thanh Hóa trong 2 giờ 15 phút, tương đương với 2.25 giờ.
Thời gian trở lại Hà Nội từ Thanh Hóa với vận tốc 30 km/h là:
t2 = x/30
Tổng thời gian đi lại là 11 giờ, kể cả thời gian nghỉ ở Thanh Hóa, nên ta có:
t1 + t2 + 2.25 = 11
Suy ra:
t1 + t2 = 8.75
Thay các giá trị vào phương trình ta có:
x/40 + x/30 = 8.75 - 2.25 3x/120 + 4x/120 = 6 7x/120 = 6 x = 102.86 (với đơn vị km)
Vậy, chiều dài quãng đường từ Hà Nội đến Thanh Hóa là 102.86 km.

Gọi a (km) (a > 0) là quãng đường Hà Nội - Thanh Hóa.
Thời gian lúc đi là a/40 (giờ)
Thời gian lúc về là a/30 (giờ)
Tổng thời gian đi và về không kể thời gian nghỉ ở Thanh Hóa là:
10 giờ 45 phút – 2 giờ = 8 giờ 45 phút = 8.3/4 giờ = 35/4 giờ
Theo để bài, ta có phương trình: a/40 + a/30 = 35/4
⇔ 3a/120 + 4a/120 = 1050/120 ⇔ 3a + 4a = 1050
⇔ 7a = 1050 ⇔ a = 150 (thỏa)
Vậy quãng đường Hà Nội - Thanh Hóa dài 150 km.

Bài 1:
Gọi độ dài quãng đường là x
Theo đề, ta có phương trình: x/40+x/30+2=10,75
=>x/40+x/30=8,75
hay x=150
Tham khảo:
Bài 1:
Gọi a (km) (a > 0) là quãng đường Hà Nội - Thanh Hóa.
Thời gian lúc đi là a/40 (giờ)
Thời gian lúc về là a/30 (giờ)
Tổng thời gian đi và về không kể thời gian nghỉ ở Thanh Hóa là:
10 giờ 45 phút – 2 giờ = 8 giờ 45 phút = 8.3/4 giờ = 35/4 giờ
Theo để bài, ta có phương trình: a/40 + a/30 = 35/4
⇔ 3a/120 + 4a/120 = 1050/120 ⇔ 3a + 4a = 1050
⇔ 7a = 1050 ⇔ a = 150 (thỏa)
Vậy quãng đường Hà Nội - Thanh Hóa dài 150 km.
Bài 2:
Gọi x (km) là quãng đường Hà Nội - Hải Phòng. Điều kiện: x > 0
Thời gian dự định đi:
10 giờ 30 phút - 8 giờ = 2 giờ 30 phút = 5/2 giờ
Thời gian thực tế đi:
11 giờ 20 phút - 8 giờ = 3 giờ 20 phút = 10/3 giờ
Vận tốc dự định đi: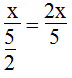
Vận tốc thực tế đi: 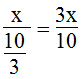
Vận tốc thực tế đi chậm hơn vận tộc dự định đi 10 km/h nên ta có phương trình:
Vậy quãng đường Hà Nội - Hải Phòng dài 100km.

Lời giải:
Tổng thời gian đi lẫn về (không tính thời gian nghỉ) là:
$10h45-2=8h45=8,75h$
Thời gian đi: $\frac{AB}{40}$
Thời gian về: $\frac{AB}{30}$
$\Rightarrow \frac{AB}{40}+\frac{AB}{30}=8,75$
$\Leftrightarrow \frac{7}{120}AB=8,75$
$\Leftrightarrow AB=150$ (km)

Thơi gian để ô tô đi đến Thanh Hóa:
10 giờ - 6 giờ 10 phút + 20 phút = 9 giờ 60 phút - 6 giờ 10 phút + 20 phút
= 3 giờ 70 phút
= \(\dfrac{19}{6}\) giờ
Độ dài quãng đường từ Hà Nội đến Thanh Hóa:
\(72\times\dfrac{19}{6}=228\left(km\right)\)