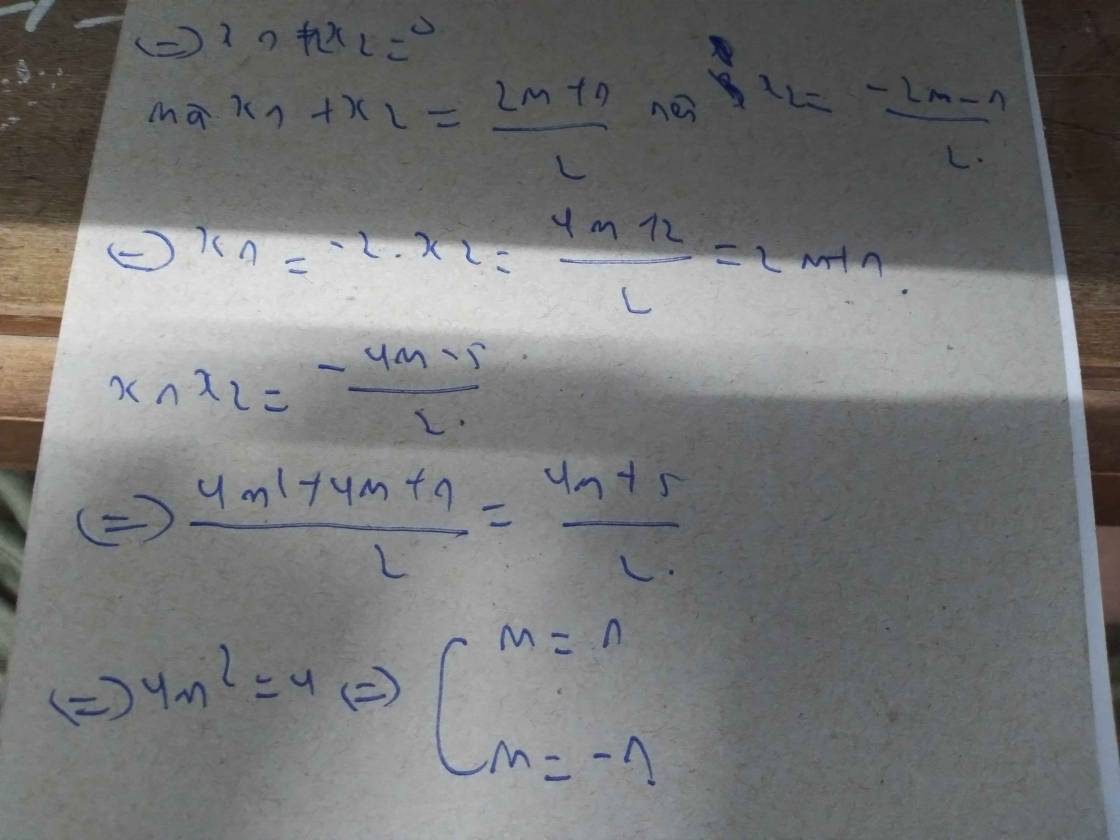Giải pt: (x+5)\sqrt{2x2+1 }=x2+x+5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NN
1
15 tháng 3 2022
a: =>7-x=0
hay x=7
b: \(\Leftrightarrow\left(x-\sqrt{2}\right)\left(x+\sqrt{2}\right)\left(x+5\right)\left(3x-8\right)=0\)
hay \(x\in\left\{\sqrt{2};-\sqrt{2};-5;\dfrac{8}{3}\right\}\)
NN
1
15 tháng 3 2022
a: =>-x+7=0
hay x=7
b: \(\Leftrightarrow\left(x-\sqrt{2}\right)\left(x+\sqrt{2}\right)\left(x+5\right)\left(3x-8\right)=0\)
hay \(x\in\left\{\sqrt{2};-\sqrt{2};-5;\dfrac{8}{3}\right\}\)
QH
1
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 10 2021
ĐKXĐ: \(x\ge-1\)
\(5\sqrt{\left(x+1\right)\left(x^2-x+1\right)}=2\left(x^2+2\right)\)
Đặt \(\left\{{}\begin{matrix}\sqrt{x+1}=a\ge0\\\sqrt{x^2-x+1}=b>0\end{matrix}\right.\)
\(\Rightarrow a^2+b^2=x^2+2\)
Phương trình trở thành:
\(5ab=2\left(a^2+b^2\right)\)
\(\Leftrightarrow2a^2-5ab+2b^2=0\)
\(\Leftrightarrow\left(2a-b\right)\left(a-2b\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2a=b\\a=2b\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}2\sqrt{x+1}=\sqrt{x^2-x+1}\\\sqrt{x+1}=2\sqrt{x^2-x+1}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}4\left(x+1\right)=x^2-x+1\\x+1=4\left(x^2-x+1\right)\end{matrix}\right.\)
\(\Leftrightarrow...\)
QH
1
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 3 2023
\(\Delta'=1-4\left(2m-4\right)>0\Rightarrow m< \dfrac{17}{8}\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-1\\x_1x_2=2m-4\end{matrix}\right.\)
Từ \(x_1+x_2=-1\Rightarrow x_2=-1-x_1\)
Thế vào \(x_1^2=2x_2+5\)
\(\Rightarrow x_1^2=2\left(-1-x_1\right)+5\)
\(\Leftrightarrow x_1^2+2x_1-3=0\)
\(\Rightarrow\left[{}\begin{matrix}x_1=1\Rightarrow x_2=-2\\x_1=-3\Rightarrow x_2=2\end{matrix}\right.\)
Thế vào \(x_1x_2=2m-4\)
\(\Rightarrow\left[{}\begin{matrix}2m-4=-2\\2m-4=-6\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}m=1\\m=-1\end{matrix}\right.\) (thỏa mãn)
Y
24 tháng 6 2023
\(\left(2-\sqrt{5}\right)x^2+\left(6-\sqrt{5}\right)x-8+2\sqrt{5}=0\)
\(\Leftrightarrow\left(2-\sqrt{5}\right)x^2-\left(2-\sqrt{5}\right)x+\left(8-2\sqrt{5}\right)x-(8-2\sqrt{5})=0\)
\(\Leftrightarrow\left(2-\sqrt{5}\right)x\left(x-1\right)+\left(8-2\sqrt{5}\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left[\left(2-\sqrt{5}\right)x+\left(8-2\sqrt{5}\right)\right]=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\\left(2-\sqrt{5}\right)x=-8+2\sqrt{5}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{-8+2\sqrt{5}}{2-\sqrt{5}}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=6+4\sqrt{5}\end{matrix}\right.\)
Vậy \(S=\left\{1;6+4\sqrt{5}\right\}\)
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 12 2020
ĐKXĐ: \(x\ge-5\)
\(\Leftrightarrow\left(x+7\right)^2-2\left(x+7\right)\sqrt{x+5}+x+5-16=0\)
\(\Leftrightarrow\left(x+7-\sqrt{x+5}\right)^2-16=0\)
\(\Leftrightarrow\left(x+7-\sqrt{x+5}-4\right)\left(x+7-\sqrt{x+5}+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x+5}=x+3\left(x\ge-3\right)\\\sqrt{x+5}=x+11\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x+5=x^2+6x+9\\x+5=x^2+22x+121\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2+5x+4=0\\x^2+21x+116=0\left(vn\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=-4< -3\left(l\right)\end{matrix}\right.\)
