Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Δ=(-m)^2-4(2m-3)
=m^2-8m+12
=(m-2)(m-6)
Để phương trình co 2 nghiệm pb thì (m-2)(m-6)>0
=>m>6 hoặc m<2
x1^2*x2+x1*x2^2=5
=>x1x2(x1+x2)=5
=>(2m-3)*m=5
=>2m^2-3m-5=0
=>2m^2-5m+2m-5=0
=>(2m-5)(m+1)=0
=>m=5/2(loại) hoặc m=-1(nhận)

Δ=(2m)^2-4(-2m-1)
=4m^2+8m+4=(2m+2)^2
Để pt có hai nghiệm pb thì 2m+2<>0
=>m<>-1
x1+x2=-2m; x1x2=-2m-1
x1^2+x2^2=(x1+x2)^2-2x1x2
=(-2m)^2-2(-2m-1)
=4m^2+4m+2
\(\dfrac{6}{x1}=\dfrac{x1+1}{x2}\)
=>x1^2+x1-6x2=0
=>4m^2+4m+2-x2^2+-2m-x2-6x2=0
=>-x2^2-7x2+4m^2+2m+2=0
=>\(x_2^2+7x_2-4m^2-2m-2=0\)(1)
\(\text{Δ}=7^2-4\left(-4m^2-2m-2\right)\)
\(=49+16m^2+8m+8\)
=16m^2+8m+57
=16m^2+8m+1+56=(4m+1)^2+56>=56>0
=>(1)luôn có nghiệm

a, Thay m = 2 vào pt ta được :
x2 - (2.2 + 1)x + 22 + 1 = 0
<=> x2 - 5x + 5 = 0
Ta có \(\Delta=b^2-4ac\)
= 25 - 20 = 5
=> \(\sqrt{\Delta}\) = \(\sqrt{5}\)
=> Pt có 2 nghiệm phân biệt \(\left[{}\begin{matrix}x_1=\dfrac{-b+\sqrt{\Delta}}{2a}\\x_2=\dfrac{-b-\sqrt{\Delta}}{2a}\end{matrix}\right.\)
<=> \(\left[{}\begin{matrix}x_1=\dfrac{5+\sqrt{5}}{2}\\x_2=\dfrac{5-\sqrt{5}}{2}\end{matrix}\right.\)
b, Để pt (*) có hai nghiệm phân biệt
<=> \(\Delta\) \(\ge\) 0
<=> (2m - 1)2 - 4(m2 + 1) \(\ge\) 0
<=> 4m2 - 4m + 1 - 4m2 - 4 \(\ge\) 0
<=> -4m - 3 \(\ge\) 0
<=> m \(\ge\dfrac{-3}{4}\)


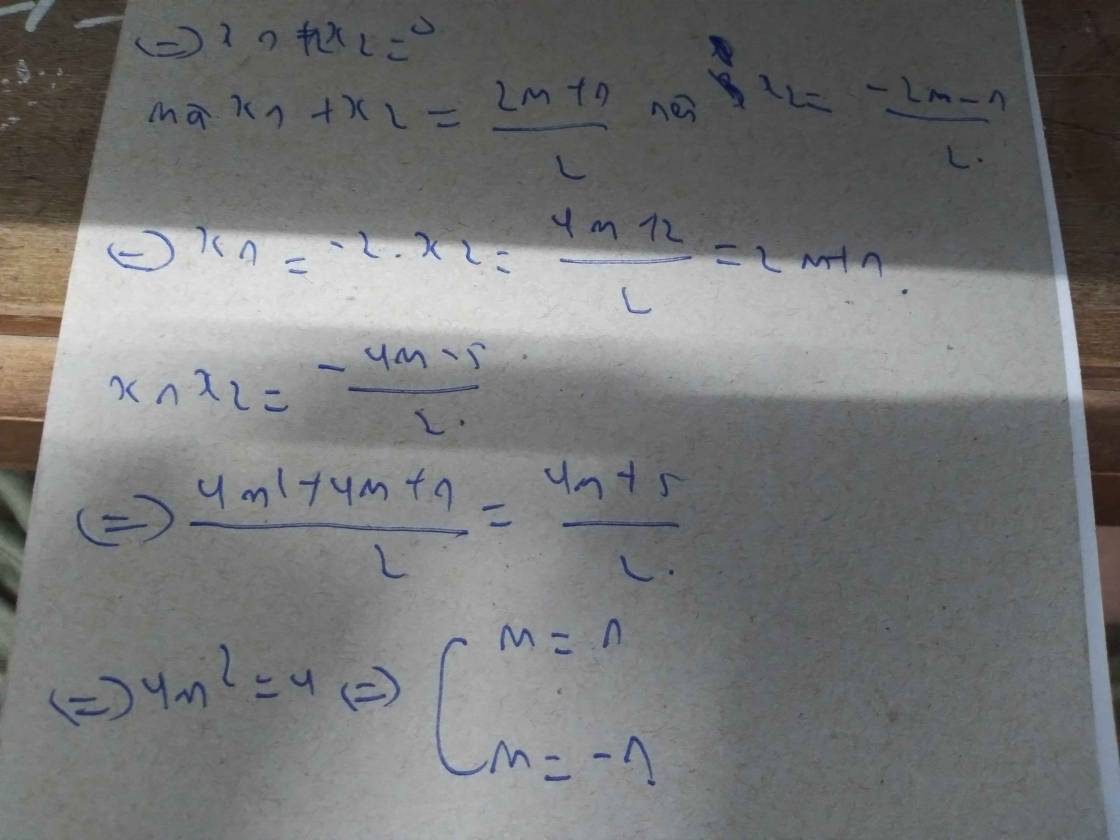
\(\Delta'=1-4\left(2m-4\right)>0\Rightarrow m< \dfrac{17}{8}\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-1\\x_1x_2=2m-4\end{matrix}\right.\)
Từ \(x_1+x_2=-1\Rightarrow x_2=-1-x_1\)
Thế vào \(x_1^2=2x_2+5\)
\(\Rightarrow x_1^2=2\left(-1-x_1\right)+5\)
\(\Leftrightarrow x_1^2+2x_1-3=0\)
\(\Rightarrow\left[{}\begin{matrix}x_1=1\Rightarrow x_2=-2\\x_1=-3\Rightarrow x_2=2\end{matrix}\right.\)
Thế vào \(x_1x_2=2m-4\)
\(\Rightarrow\left[{}\begin{matrix}2m-4=-2\\2m-4=-6\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}m=1\\m=-1\end{matrix}\right.\) (thỏa mãn)