chứng minh rằng
cos2x.(2sin2x + cos2x) = 1 - 4sin4x
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LT
1
KR
3 tháng 8 2019
cos2x = 1- sin^x
sin2x= 2sinxcosx
Nhóm lại bình thường và giải thôi
PT
1
PT
1
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 4 2020
a/ \(y'=\frac{\left(2cos2x-2sin2x\right)\left(2sin2x-cos2x\right)-\left(sin2x+cos2x\right)\left(4cos2x+2sin2x\right)}{\left(2sin2x-cos2x\right)^2}\)
\(=\frac{3sin4x-2cos^22x-4sin^22x-3sin4x-2sin^22x-4cos^22x}{\left(2sin2x-cos2x\right)^2}\)
\(=\frac{-6cos^22x-6sin^22x}{\left(2sin2x-cos2x\right)^2}=-\frac{6}{\left(2sin2x-cos2x\right)^2}\)
b/ \(y'=4cosx.cos5x.sin6x+4sinx\left(cos5x.sin6x\right)'\)
\(=4cosx.cos5x.sin6x+4sinx\left(-5sin5x.sin6x+6cos5x.cos6x\right)\)
\(=4cosx.cos5x.sin6x+4sinx\left(6cos11x+sin5x.sin6x\right)\)
\(=4sin6x\left(cosx.cos5x+sinx.sinx\right)+24sinx.cos11x\)
\(=4sin6x.cos4x+24sinx.cos11x\)
c/ \(y'=\frac{\left(2cos2x-2sin2x\right)\left(sin2x-cos2x\right)-\left(sin2x-cos2x\right)\left(2cos2x+2sin2x\right)}{\left(sin2x-cos2x\right)^2}\)
\(=\frac{-2\left(sin2x-cos2x\right)^2-2\left(sin2x-cos2x\right)\left(sin2x+cos2x\right)}{\left(sin2x-cos2x\right)^2}\)
\(=\frac{-2\left(sin2x-cos2x\right)-2\left(sin2x+cos2x\right)}{sin2x-cos2x}=\frac{-4sin2x}{sin2x-cos2x}\)
CM
21 tháng 8 2018
cos2(x + kπ) = cos(2x + k2π) = cos2x, k ∈ Z.
Vậy hàm số y = cos 2x là hàm số chẵn, tuần hoàn, có chu kì là π.
Đồ thị hàm số y = cos2x
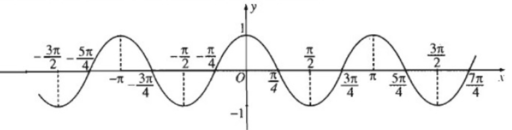
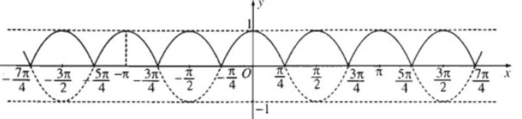
Đồ thị hàm số y = |cos2x|
16 tháng 8 2021
a) <=> 4sinxcosx -(2cos2x-1)=7sinx+2cosx-4
<=> 2cos2x+(2-4sinx)cosx+7sinx-5=0
- sinx=1 => 2cos2x-2cosx+2=0
pt trên vn
16 tháng 8 2021
b) <=> 2sinxcosx-1+2sin2x+3sinx-cosx-1=0
<=> cos(2sinx-1)+2sin2x+3sinx-2=0
<=> cosx(2sinx-1)+(2sinx-1)(sinx+2)=0
<=> (2sinx-1)(cosx+sinx+2)=0
<=> sinx=1/2 hoặc cosx+sinx=-2(vn)
<=> x= \(\frac{\pi}{6}+k2\pi\) hoặc \(x=\frac{5\pi}{6}+k2\pi\left(k\in Z\right)\)
NT
1
NV
Nguyễn Việt Lâm
Giáo viên
3 tháng 10 2021
ĐKXĐ: \(sin2x\ne-\dfrac{1}{2}\)
\(5\left(sinx+\dfrac{3sinx-4sin^3x+4cos^3x-3cosx}{1+2sin2x}\right)=cos2x+3\)
\(\Leftrightarrow5\left(sinx+\dfrac{3\left(sinx-cosx\right)-4\left(sinx-cosx\right)\left(1+\dfrac{1}{2}sin2x\right)}{1+2sin2x}\right)=cos2x+3\)
\(\Leftrightarrow5\left(sinx+\dfrac{\left(sinx-cosx\right)\left(-1-2sin2x\right)}{1+2sin2x}\right)=cos2x+3\)
\(\Leftrightarrow5\left(sinx+cosx-sinx\right)=cos2x+3\)
\(\Leftrightarrow5cosx=2cos^2x-1+3\)
\(\Leftrightarrow...\)
17 tháng 8 2020
\(2\sin2x-\cos2x=7\sin x+2\cos x-4\)
\(\Rightarrow4\sin x\cos x-\left(1-2\sin^2x\right)-7\sin x-2\cos x+4=0\)
\(\Rightarrow2\cos x\left(2\sin x-1\right)+\left(2\sin^2-7\sin x+3\right)=0\)
\(\Rightarrow2\cos x\left(2\sin x-1\right)+\left(2\sin x-1\right)\left(\sin x-3\right)=0\)
\(\Rightarrow\left(2\sin x-1\right)\left(2\cos x+\sin x-3\right)=0\)
\(\Rightarrow\orbr{\begin{cases}2\sin x-1=0\\2\cos x+\sin x=3,\left(vn\right)\end{cases}\Rightarrow\orbr{\begin{cases}x=\frac{\eta}{6}+k2\eta\\x=\frac{5\eta}{6}+k2\eta\end{cases}}}\)
\(\eta=Pi;3.14159\)
PT
1
CM
13 tháng 10 2018
2 sin 2 x + sin x . cos x - cos 2 x = 3 ⇒ tan 2 x – tan x + 4 = 0
Phương trình vô nghiệm
\(cos^2x\left(2sin^2x+cos^2x\right)=\left(1-sin^2x\right)\left(sin^2x+cos^2x+sin^2x\right)\)
\(=\left(1-sin^2x\right)\left(1+sin^2x\right)=1-sin^4x\)