Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
y = cos6 x+ sin2xcos2x(sin2x + cos2x) + sin4x - sin2x
= cos6x + sin2x(1 - sin2x) + sin4x - sin2x = cos6x
Do đó : y' = -6cos5xsinx.

Chọn D
y ' = sin 2 x + cos 2 x / . 2 sin 2 x − cos 2 x − 2 sin 2 x − cos 2 x / . sin 2 x + cos 2 x 2 sin 2 x − cos 2 x 2
y ' = 2 cos 2 x − 2 sin 2 x 2 sin 2 x − cos 2 x − 4 cos 2 x + 2 sin 2 x sin 2 x + cos 2 x 2 sin 2 x − cos 2 x 2 = 4. c os2x. sin2x - 2cos 2 2 x − 4 sin 2 2 x + 2. sin 2 x . c os2x ( 2 sin 2 x − cos 2 x ) 2 − ( 4cos2x . sin2x + 4cos 2 2 x + 2 sin 2 2 x + 2 sin 2 x . c os2x ( 2 sin 2 x − c os2x) 2
y ' = − 6 cos 2 2 x − 6 sin 2 2 x 2 sin 2 x − cos 2 x 2 = − 6 2 sin 2 x − cos 2 x 2

a)\(y=\sqrt{3}sinx+cosx=2\left(\dfrac{\sqrt{3}}{2}sinx+\dfrac{1}{2}cosx\right)\)\(=2\left(sinx.cos\dfrac{\pi}{6}+cosx.sin\dfrac{\pi}{6}\right)\)\(=2sin\left(x+\dfrac{\pi}{6}\right)\)
Có \(-1\le sin\left(x+\dfrac{\pi}{6}\right)\le1\) \(\Leftrightarrow-2\le2sin\left(x+\dfrac{\pi}{6}\right)\le2\)
\(\Leftrightarrow-2\le y\le2\)
miny=-2 \(\Leftrightarrow sin\left(x+\dfrac{\pi}{6}\right)=-1\) \(\Leftrightarrow x+\dfrac{\pi}{6}=-\dfrac{\pi}{2}+2k\pi\left(k\in Z\right)\) \(\Leftrightarrow x=-\dfrac{2\pi}{3}+k2\pi\left(k\in Z\right)\)
maxy=2\(\Leftrightarrow sin\left(x+\dfrac{\pi}{6}\right)=1\) \(\Leftrightarrow x+\dfrac{\pi}{6}=\dfrac{\pi}{2}+k2\pi\left(k\in Z\right)\)\(\Leftrightarrow x=\dfrac{\pi}{3}+k2\pi\left(k\in Z\right)\)
b) \(y=sin2x-cos2x=\sqrt{2}sin\left(2x-\dfrac{\pi}{4}\right)\)
Có \(\sqrt{2}\ge\sqrt{2}sin\left(2x-\dfrac{\pi}{4}\right)\ge-\sqrt{2}\)
\(\Leftrightarrow\sqrt{2}\ge y\ge-\sqrt{2}\)
miny=\(-\sqrt{2}\) \(\Leftrightarrow sin\left(2x-\dfrac{\pi}{4}\right)=-1\)\(\Leftrightarrow2x-\dfrac{\pi}{4}=-\dfrac{\pi}{2}+k2\pi\left(k\in Z\right)\)\(\Leftrightarrow x=-\dfrac{\pi}{8}+k\pi\left(k\in Z\right)\)
maxy=\(\sqrt{2}\Leftrightarrow sin\left(2x-\dfrac{\pi}{4}\right)=1\)\(\Leftrightarrow x=\dfrac{3\pi}{8}+k\pi\left(k\in Z\right)\)
c) \(y=3sinx+4cosx=5\left(\dfrac{3}{5}sinx+\dfrac{4}{5}cosx\right)\)
Đặt \(cosa=\dfrac{3}{5}\) và \(sina=\dfrac{4}{5}\)(vì cos2a+sin2a=1)
\(y=5\left(sinx.cosa+cosx.sina\right)\)\(=5sin\left(x+a\right)\)
\(\Rightarrow-5\le y\le5\)
miny=-5 <=> \(sin\left(x+a\right)=-1\)\(\Leftrightarrow x=-\dfrac{\pi}{2}-arc.sina+k2\pi\left(k\in Z\right)\)
maxy=5 <=> \(sin\left(x+a\right)=1\)\(\Leftrightarrow x=\dfrac{\pi}{2}-arc.sina+k2\pi\left(k\in Z\right)\)
(P/s1:cái x ở câu c ấy trông nó ngu ngu??
P/s2:sau khi load lại câu hỏi ở 1 tab khác ,thấy 1 câu trả lời nhưng vẫn đăng vì cảm thấy bỏ đi hơi phí :?)
Áp dụng quy tắc sau: Nếu \(a\sin x+b\cos y=c\Leftrightarrow a^2+b^2\ge c^2\)
a/ \(3+1\ge y^2\Leftrightarrow4\ge y^2\Leftrightarrow-2\le y\le2\)
\(y_{max}=2\Leftrightarrow\sqrt{3}\sin x+\cos x=2\Leftrightarrow\dfrac{\sqrt{3}}{2}\sin x+\dfrac{1}{2}\cos x=1\Leftrightarrow\cos\dfrac{\pi}{6}.\sin x+\sin\dfrac{\pi}{6}.\cos x=1\)
\(\Rightarrow\sin\left(x+\dfrac{\pi}{6}\right)=1\Leftrightarrow x+\dfrac{\pi}{6}=\dfrac{\pi}{2}+k2\pi\Leftrightarrow x=\dfrac{\pi}{3}+k2\pi\)
\(y_{min}=-2\Leftrightarrow\sin\left(x+\dfrac{\pi}{6}\right)=-1\Leftrightarrow x+\dfrac{\pi}{6}=-\dfrac{\pi}{2}+k2\pi\Leftrightarrow x=-\dfrac{2}{3}\pi+k2\pi\)

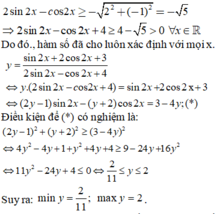
a/ \(y'=\frac{\left(2cos2x-2sin2x\right)\left(2sin2x-cos2x\right)-\left(sin2x+cos2x\right)\left(4cos2x+2sin2x\right)}{\left(2sin2x-cos2x\right)^2}\)
\(=\frac{3sin4x-2cos^22x-4sin^22x-3sin4x-2sin^22x-4cos^22x}{\left(2sin2x-cos2x\right)^2}\)
\(=\frac{-6cos^22x-6sin^22x}{\left(2sin2x-cos2x\right)^2}=-\frac{6}{\left(2sin2x-cos2x\right)^2}\)
b/ \(y'=4cosx.cos5x.sin6x+4sinx\left(cos5x.sin6x\right)'\)
\(=4cosx.cos5x.sin6x+4sinx\left(-5sin5x.sin6x+6cos5x.cos6x\right)\)
\(=4cosx.cos5x.sin6x+4sinx\left(6cos11x+sin5x.sin6x\right)\)
\(=4sin6x\left(cosx.cos5x+sinx.sinx\right)+24sinx.cos11x\)
\(=4sin6x.cos4x+24sinx.cos11x\)
c/ \(y'=\frac{\left(2cos2x-2sin2x\right)\left(sin2x-cos2x\right)-\left(sin2x-cos2x\right)\left(2cos2x+2sin2x\right)}{\left(sin2x-cos2x\right)^2}\)
\(=\frac{-2\left(sin2x-cos2x\right)^2-2\left(sin2x-cos2x\right)\left(sin2x+cos2x\right)}{\left(sin2x-cos2x\right)^2}\)
\(=\frac{-2\left(sin2x-cos2x\right)-2\left(sin2x+cos2x\right)}{sin2x-cos2x}=\frac{-4sin2x}{sin2x-cos2x}\)