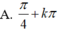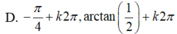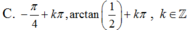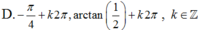K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DT
3
NV
Nguyễn Việt Lâm
Giáo viên
31 tháng 7 2020
c/
\(\Leftrightarrow1+2cos^2x-1+cosx=0\)
\(\Leftrightarrow2cos^2x-cosx=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=0\\cosx=\frac{1}{2}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{2}+k\pi\\x=\pm\frac{\pi}{3}+k2\pi\end{matrix}\right.\)
d/
Đặt \(\left\{{}\begin{matrix}\left|sinx\right|=a\ge0\\cosx=b\end{matrix}\right.\) ta được hệ:
\(\left\{{}\begin{matrix}a+3b=2\\a^2+b^2=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=2-3b\\a^2+b^2=1\end{matrix}\right.\)
\(\Rightarrow\left(2-3b\right)^2+b^2-1=0\)
\(\Rightarrow10b^2-12b+3=0\Rightarrow\left[{}\begin{matrix}b=\frac{6+\sqrt{6}}{10}\Rightarrow a=\frac{2-3\sqrt{6}}{10}\left(l\right)\\b=\frac{6-\sqrt{6}}{10}\Rightarrow a=\frac{2+3\sqrt{6}}{10}\end{matrix}\right.\)
\(\Rightarrow cosx=\frac{6-\sqrt{6}}{10}\)
\(\Rightarrow x=\pm arccos\left(\frac{6-\sqrt{6}}{10}\right)+k2\pi\)
NV
Nguyễn Việt Lâm
Giáo viên
31 tháng 7 2020
b/
\(cos\left(8sinx\right)=1\)
\(\Leftrightarrow8sinx=k2\pi\)
\(\Leftrightarrow sinx=\frac{k\pi}{4}\)
Do \(-1\le sinx\le1\Rightarrow-1\le\frac{k\pi}{4}\le1\)
\(\Rightarrow k=\left\{-1;0;1\right\}\)
\(\Rightarrow\left[{}\begin{matrix}sinx=-\frac{\pi}{4}\\sinx=0\\sinx=\frac{\pi}{4}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\pm arcsin\left(\frac{\pi}{4}\right)+k2\pi\\x=\pi\pm arcsin\left(\frac{\pi}{4}\right)+k2\pi\\x=k\pi\end{matrix}\right.\)
CM
10 tháng 10 2018
Hướng dẫn giải
Chọn C.
TH1: Nếu cosx =0 có sin2x = 1 không thỏa mãn phương trình.
TH2: 
chia cả hai vế của phương trình cho cos2x ta được:
NV
Nguyễn Việt Lâm
Giáo viên
29 tháng 9 2020
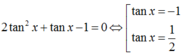
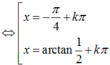
a/ \(4cos^3x-3cosx-4\left(2cos^2x-1\right)+3cosx-4=0\)
\(\Leftrightarrow4cos^3x-8cos^2x=0\)
\(\Leftrightarrow4cos^2x\left(cosx-2\right)=0\)
\(\Leftrightarrow cosx=0\Rightarrow x=\frac{\pi}{2}+k\pi\)
\(0< \frac{\pi}{2}+k\pi< 14\Rightarrow-\frac{1}{2}< k< \frac{14-\frac{\pi}{2}}{\pi}\Rightarrow k=\left\{0;1;2;3\right\}\)
\(\Rightarrow x=\left\{\frac{\pi}{2};\frac{3\pi}{2};\frac{5\pi}{2};\frac{7\pi}{2}\right\}\)
b/ Bạn coi lại đề, cái ngoặc thứ 2 thiếu \(\left(2cos\left(???\right)+cosx\right)\)
c/ Bạn coi lại đề, có 2 số hạng \(cos2x\) xuất hiện ở vế trái, cấp 3 chắc ko ai cho kiểu vậy đâu, nếu đúng thế thì người ta cộng luôn thành \(2cos2x\) cho rồi
