-Khối cầu đặc đồng chất tâm O, bán kính R, khối lượng m phân bố đều, Người ta khoét bên trong khối cầu đó một lỗ hổng cũng có dạng hình cầu tâm O', bán kính r = R/2. biết O cách O' 1 đoạn d =R/2. tinh momen quán tính của các phần còn lại của khối cầu đối với trục quay trong các trường hợp :
- Chứa O và O'.
- Chứa O và vuông góc với OO'
- Chứa O' và vuông góc với OO'
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
Phần khoét đi, nếu đặt lại chỗ cũ sẽ hút m lực hấp dẫn:
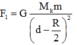
Lực hấp dẫn do cả quả cầu đặc tác dụng lên m:
![]()
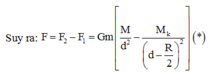
Do quả cầu đồng chất nên:
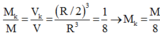
Thay vào (*) rồi biến đổi ta được
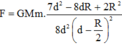

Đáp án A.
Phần khoát đi, nếu đặt lại chỗ cũ sẽ hút m lực hấp dẫn: F 1 = G M k m ( d - R 2 ) 2
Lực hấp dẫn do cả quả cầu đặc tác dụng lên m: F 2 = G M m d 2
Suy ra:
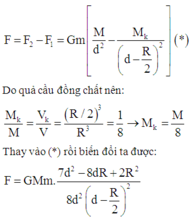

Đáp án A.
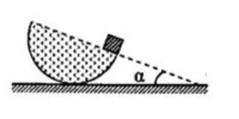
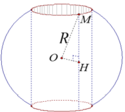
Gọi I là tâm của đường tròn dáy của chỏm cầu. M là 1 đỉnh của hình hộp thuộc đường tròn I ; R 2 .
Ta có:
I M = R 2 ; O M = R ⇒ O I = R 2 − R 2 4 = 3 R 2 .
Do đó khối hộp có chiều cao là
h = 3 R = 10 3 .
Thể tích của chỏm cầu bị cắt:
V = ∫ h 2 R π R 2 − x 2 d x = ∫ 5 3 10 π 100 − x 2 d x ≃ 53 , 87.
Thể tích của khối hộp chữ nhật:
V = S d . h = R 2 2 . 3 . R = 3 2 R 3 ≃ 866 , 025.
Thể tích khối cầu ban đầu:
V = 4 3 π R 3 ≃ 4188 , 79.
Do đó thể tích cần tính:
V ≃ 4188 , 79 − 866 , 025 − 2.53 , 87 ≃ 3215 , 023.

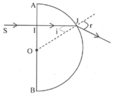
+ Tia sáng đi thẳng qua mặt phẳng AB của khối bán cầu, tới mặt cầu tại J với góc tới là i.

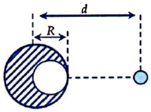
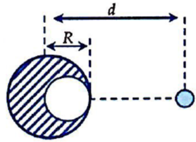
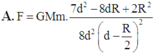
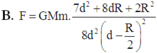
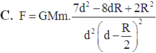



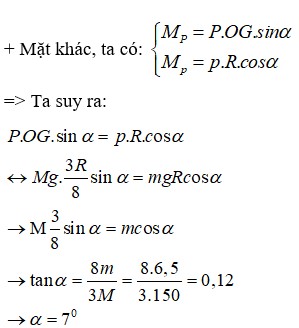
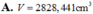
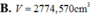
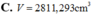

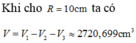
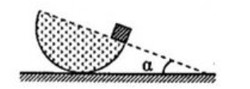


Ý tưởng chung là "bù" phần bị khoét, coi như nó đặc, như vậy ta luôn có \(I_O+I_{O'}=I_C\) với \(I_C\) là mômen quán tính của hình cầu đặc hoàn hảo khi chưa bị khoét \(\Rightarrow I_O=I_C-I_{O'}\)
Ta có khối lượng đã bị khoét:
\(\frac{m'}{m}=\left(\frac{r}{R}\right)^3\Rightarrow m'=\frac{m}{8}\)
TH1: Trục quay qua \(OO':\)
\(I_O=I_C-I_{O'}=\frac{2}{5}mR^2-\frac{2}{5}m'.r=\frac{2}{5}mR^2-\frac{2}{5}.\frac{m}{8}.\left(\frac{R}{2}\right)^2=\frac{31}{80}mR^2\)
TH2: Chứa O và vuông góc OO':
Áp dụng định lý Steiner-Huyghen, momen quán tính của phần tưởng tượng \(O'\) với trục qua O và vuông góc OO':
\(I_{O'}=\frac{2}{5}\frac{m}{8}\left(\frac{R}{2}\right)^2+\frac{m}{8}.\left(\frac{R}{2}\right)^2=\frac{7}{160}mR^2\)
\(\Rightarrow I_O=I_C-I_{O'}=\frac{2}{5}mR^2-\frac{7}{160}mR^2=\frac{57}{160}mR^2\)
- TH3: Chứa O' và vuông góc OO':
Áp dụng định lý Steiner-Huyghen, momen của khối chưa bị khoét \(I_C\) với trục mới:
\(I_C=\frac{2}{5}mR^2+m.\left(\frac{R}{2}\right)^2=\frac{13}{20}mR^2\)
\(\Rightarrow I_O=I_C-I_{O'}=\frac{13}{20}mR^2-\frac{2}{5}.\frac{m}{8}.\left(\frac{R}{2}\right)^2=\frac{51}{80}mR^2\)
...