Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A.
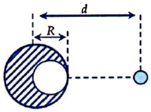
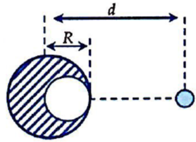
Phần khoát đi, nếu đặt lại chỗ cũ sẽ hút m lực hấp dẫn: F 1 = G M k m ( d - R 2 ) 2
Lực hấp dẫn do cả quả cầu đặc tác dụng lên m: F 2 = G M m d 2
Suy ra:
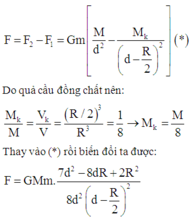

Có hình ko bạn? Đề bài ko có dấu chấm dấu phẩy nên đọc ko hiểu gì :v

Ý tưởng chung là "bù" phần bị khoét, coi như nó đặc, như vậy ta luôn có \(I_O+I_{O'}=I_C\) với \(I_C\) là mômen quán tính của hình cầu đặc hoàn hảo khi chưa bị khoét \(\Rightarrow I_O=I_C-I_{O'}\)
Ta có khối lượng đã bị khoét:
\(\frac{m'}{m}=\left(\frac{r}{R}\right)^3\Rightarrow m'=\frac{m}{8}\)
TH1: Trục quay qua \(OO':\)
\(I_O=I_C-I_{O'}=\frac{2}{5}mR^2-\frac{2}{5}m'.r=\frac{2}{5}mR^2-\frac{2}{5}.\frac{m}{8}.\left(\frac{R}{2}\right)^2=\frac{31}{80}mR^2\)
TH2: Chứa O và vuông góc OO':
Áp dụng định lý Steiner-Huyghen, momen quán tính của phần tưởng tượng \(O'\) với trục qua O và vuông góc OO':
\(I_{O'}=\frac{2}{5}\frac{m}{8}\left(\frac{R}{2}\right)^2+\frac{m}{8}.\left(\frac{R}{2}\right)^2=\frac{7}{160}mR^2\)
\(\Rightarrow I_O=I_C-I_{O'}=\frac{2}{5}mR^2-\frac{7}{160}mR^2=\frac{57}{160}mR^2\)
- TH3: Chứa O' và vuông góc OO':
Áp dụng định lý Steiner-Huyghen, momen của khối chưa bị khoét \(I_C\) với trục mới:
\(I_C=\frac{2}{5}mR^2+m.\left(\frac{R}{2}\right)^2=\frac{13}{20}mR^2\)
\(\Rightarrow I_O=I_C-I_{O'}=\frac{13}{20}mR^2-\frac{2}{5}.\frac{m}{8}.\left(\frac{R}{2}\right)^2=\frac{51}{80}mR^2\)

1/
Trọng lực ở đây đóng vai trò như 1 lực hấp dẫn
Theo đề ta có trọng lượng của quả cầu ở độ cao h bằng 1/4 trọng lượng của nó trên mặt đất
\(P'=\dfrac{1}{4}\cdot P\Rightarrow G\cdot\dfrac{mM}{\left(R+h\right)^2}=\dfrac{1}{4}\cdot G\cdot\dfrac{mM}{R^2}\)
\(\Rightarrow\dfrac{1}{\left(6400\cdot1000+h\right)^2}=\dfrac{1}{4\cdot\left(6400\cdot1000\right)^2}\Rightarrow h=6400000\left(m\right)=6400\left(km\right)\)
ChọnC
2/
Theo đề ta có gia tốc rơi tự do có giá trị bằng 1/3 gia tốc rơi tự do ở mặt đất ở độ cao
\(g'=\dfrac{1}{3}g\Rightarrow G\dfrac{M}{\left(R+h\right)^2}=\dfrac{1}{3}\cdot G\dfrac{M}{R^2}\)
\(\Rightarrow\dfrac{1}{\left(6400\cdot1000+h\right)^2}=\dfrac{1}{3\cdot\left(6400\cdot1000\right)^2}\Rightarrow h=4685125,168\left(m\right)\approx4685\left(km\right)\)
Chọn B

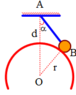
vì đề ko cho hệ số ma sát giữa M và sàn nên coi
sàn nhẵn:
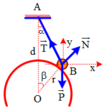
(trên hình mình ko vẽ mấy lực P, N vào vì hình sẽ bị đè)
hệ chuyển động cùng gia tốc a
các lực tác dụng vào m gồm: lực căng dây T, lực ma sát Fms1, phản lực N1, trọng lực P1
\(\overrightarrow{F_{ms}}+\overrightarrow{N_1}+\overrightarrow{P_1}+\overrightarrow{T}=m.\overrightarrow{a}\) (1)
các lực tác dụng lên M gồm: lực căng dây T, lực ma sát Fms2, lực kéo F, trọng lực P2, phản lực N2
\(\overrightarrow{F}+\overrightarrow{F_{ms2}}+\overrightarrow{P_2}+\overrightarrow{N_2}+\overrightarrow{T}=M.\overrightarrow{a}\) (2)
______
ta có \(F_{ms1}=F_{ms2}=\mu.m.g\)
chiếu (1),(2) lên chiều dương cùng chiều chuyển động của các vật
vật m: \(T-\mu.m.g=m.a\)
vật M: \(F-T-\mu.m.g=M.a\)
để vật M chuyển động với gia tốc a=\(\dfrac{g}{2}=5\)m/s2
\(\Leftrightarrow T=m.a+\mu.m.g=\)10N
\(\Rightarrow F=T+\mu.m.g+M.a\)=25N
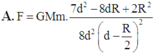
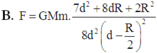
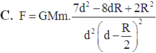

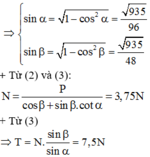
Chọn A.
Phần khoét đi, nếu đặt lại chỗ cũ sẽ hút m lực hấp dẫn:
Lực hấp dẫn do cả quả cầu đặc tác dụng lên m:
Do quả cầu đồng chất nên:
Thay vào (*) rồi biến đổi ta được