giúp mình mấy bài này với
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(B=\left(3+\dfrac{a+\sqrt{a}}{\sqrt{a}+1}\right)\left(3-\dfrac{a-\sqrt{a}}{\sqrt{a}-1}\right)\left(a\ge0,a\ne1\right)\)
\(=\left(3+\dfrac{\sqrt{a}\left(\sqrt{a}+1\right)}{\sqrt{a}+1}\right)\left(3-\dfrac{\sqrt{a}\left(\sqrt{a}-1\right)}{\sqrt{a}-1}\right)=\left(3+\sqrt{a}\right)\left(3-\sqrt{a}\right)=9-a\)
Để hàm số \(y=\left(m-1\right)x+2\) đồng biến trên R thì \(m-1>0\Rightarrow m>1\)
Câu 2:
Để hàm số y=(m-1)x+2 đồng biến trên R thì m-1>0
hay m>1

a) \(\left\{{}\begin{matrix}2x-3y=11\\5x-4y=3\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}10x-15y=55\left(1\right)\\10x-8y=6\left(2\right)\end{matrix}\right.\)
Lấy \(\left(1\right)-\left(2\right)\Rightarrow-7y=49\Rightarrow y=-7\Rightarrow2x=11+3\left(-7\right)=-10\)
\(\Rightarrow x=-5\)
b) đề nãy chỉ có 1 pt x,y không thể tính x,y được
c) bạn viết đề rõ ra chứ mờ quá đọc ko được



Bài 8:
1: =>x+1+3 chia hết cho x+1
=>\(x+1\in\left\{1;-1;3;-3\right\}\)
=>\(x\in\left\{0;-2;2;-4\right\}\)
2: =>2x+2-5 chia hết cho x+1
=>\(x+1\in\left\{1;-1;5;-5\right\}\)
=>\(x\in\left\{0;-2;4;-6\right\}\)
3: =>2x-2+3 chia hết cho x-1
=>\(x-1\in\left\{1;-1;3;-3\right\}\)
=>\(x\in\left\{2;0;4;-2\right\}\)
4: =>4x+1 chia hết cho 2x-3
=>4x-6+7 chia hết cho 2x-3
=>\(2x-3\in\left\{1;-1;7;-7\right\}\)
=>\(x\in\left\{2;1;5;-2\right\}\)

a: Vì x>=10 nên x-10>=0
=>A=x-10
b: Vì x>=9 nên x-9>=0
=>9-x<=0
=>A=x-9
c: Vì x<3 nên 2x-6<0
=>C=6-2x



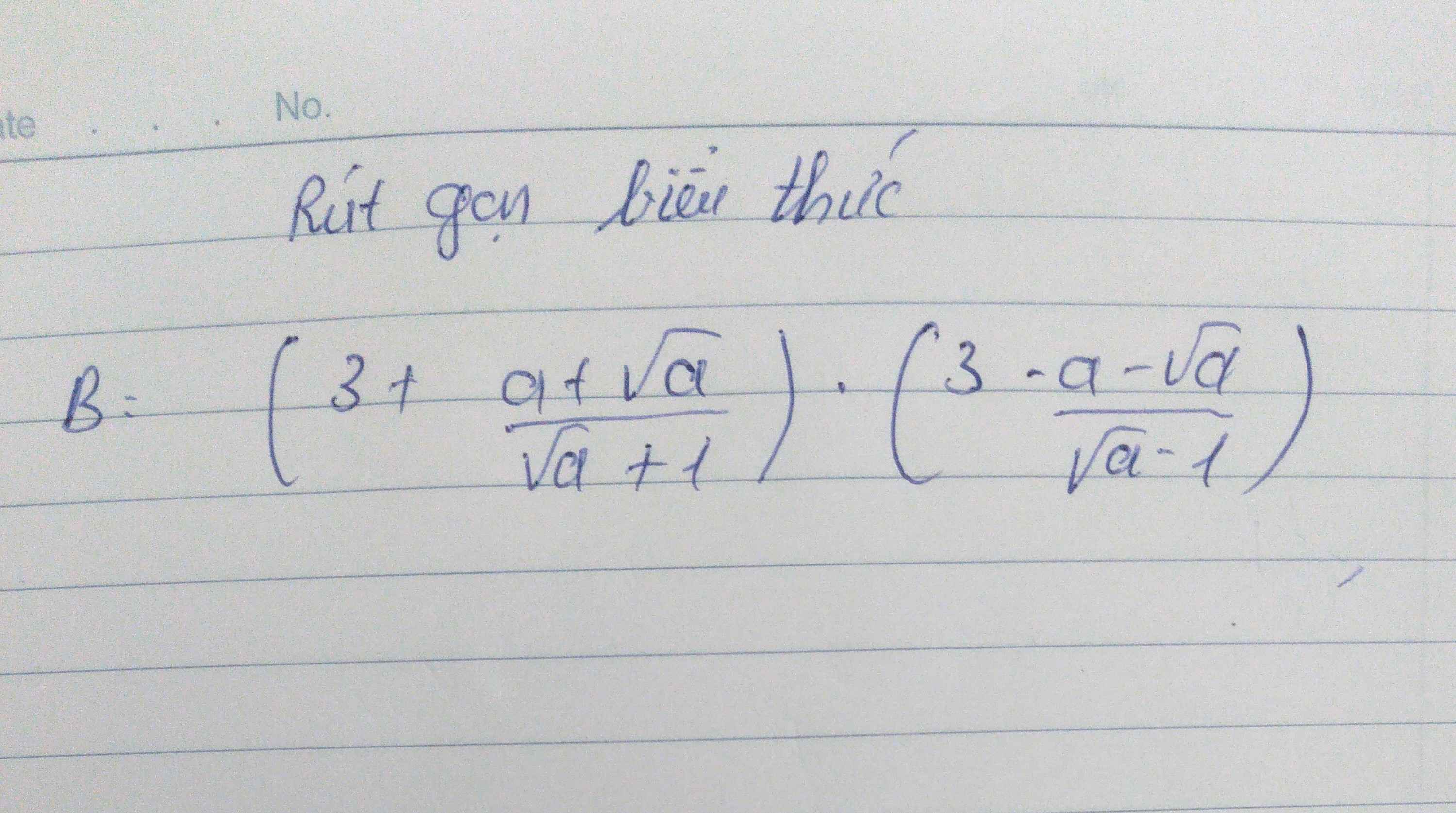
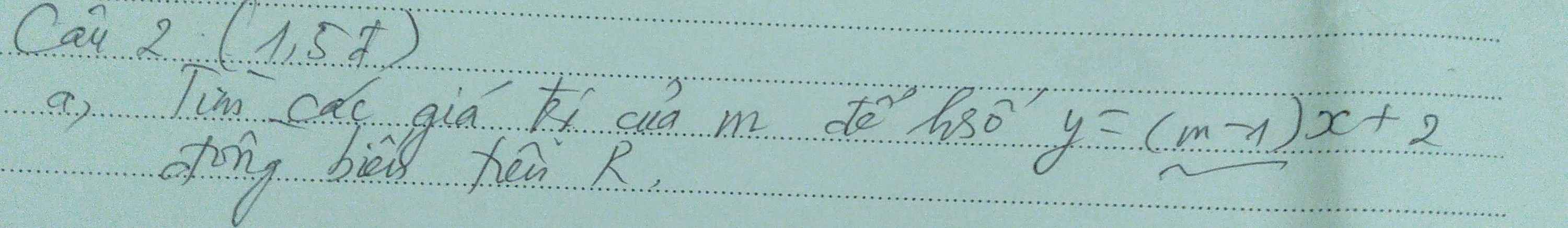

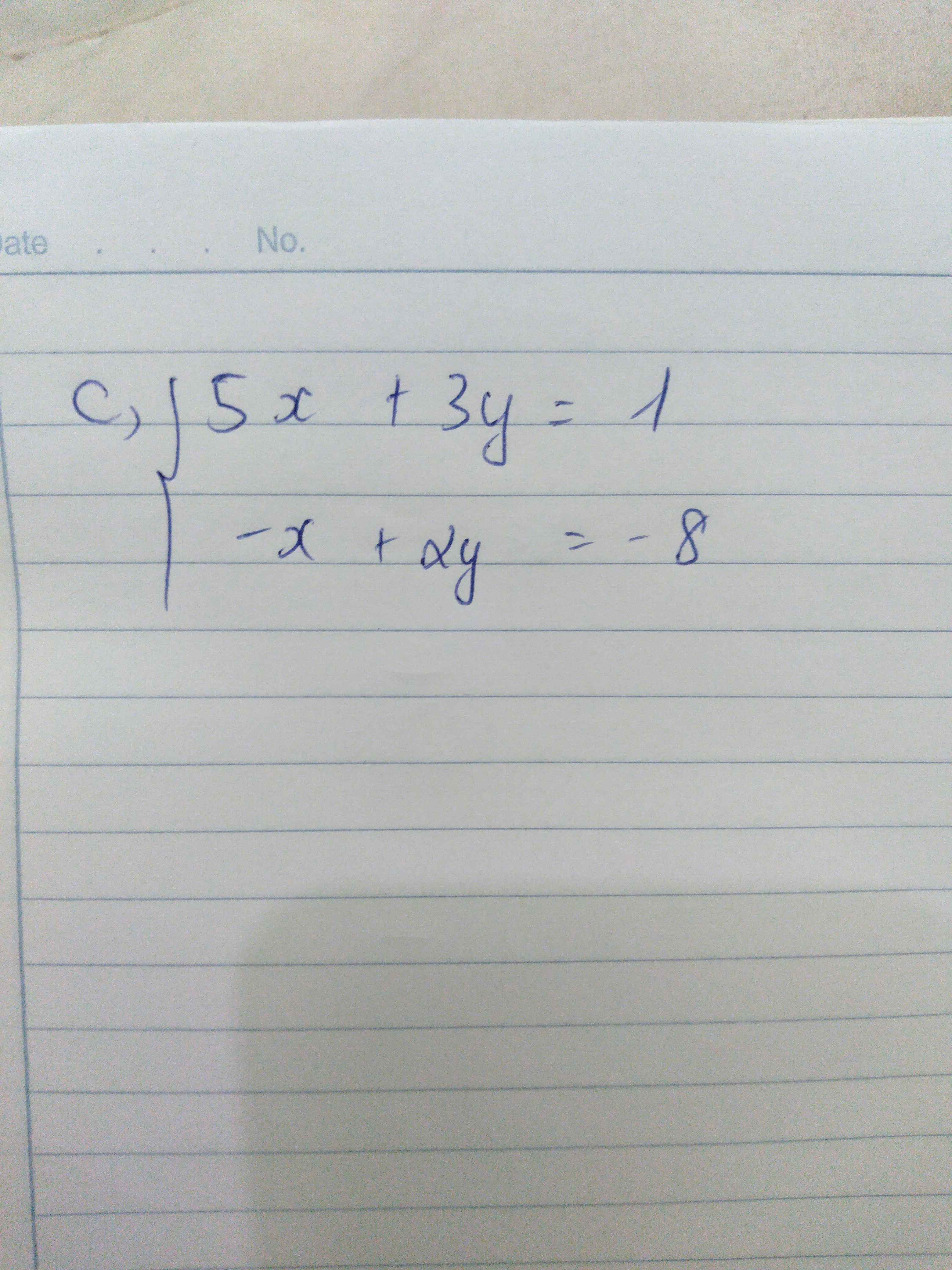




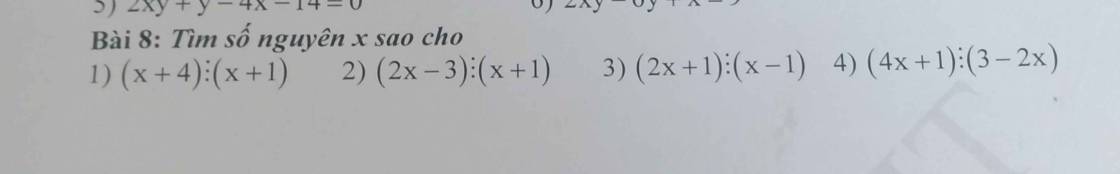

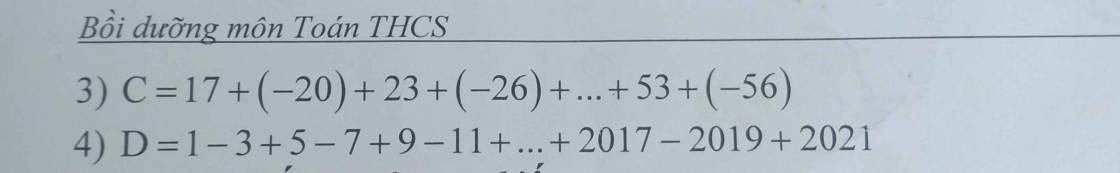
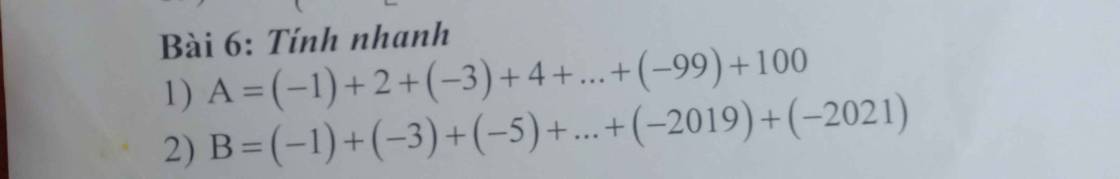
 mấy bn giúp mình bài này với
mấy bn giúp mình bài này với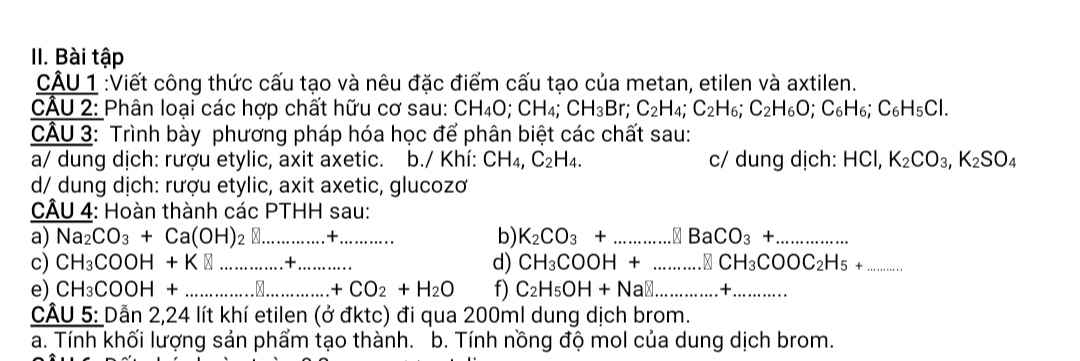





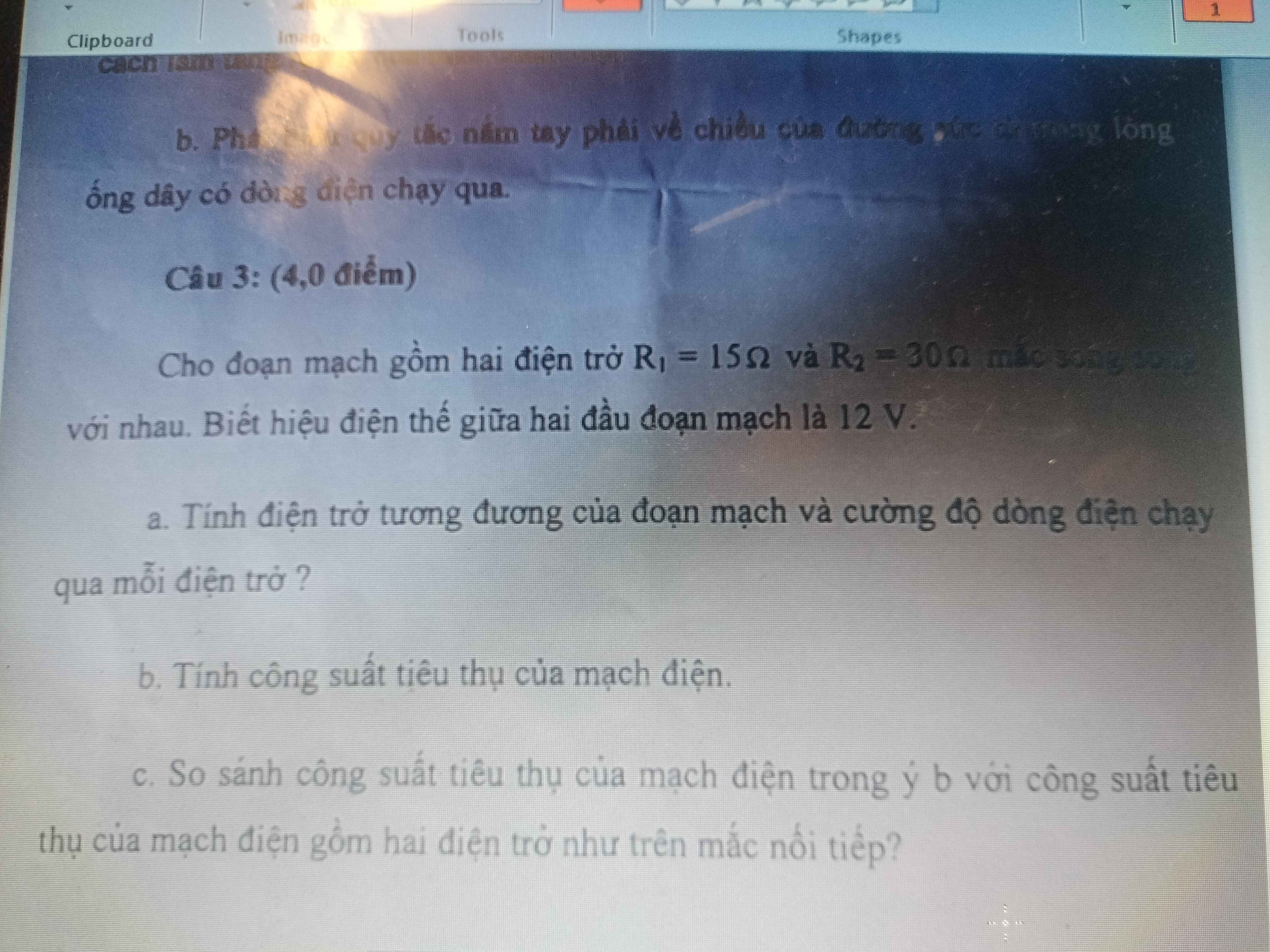
Câu 45:
Đặt \(g\left(x\right)=\frac{x}{x^2+x+1}-\frac{m}{3}\)
\(g'\left(x\right)=\left(\frac{x}{x^2+x+1}\right)'=\frac{-x^2+1}{\left(x^2+x+1\right)^2}\)
\(g'\left(x\right)=0\Rightarrow x=\pm1\), \(g'\left(x\right)\)xác định với mọi \(x\inℝ\).
Suy ra để hàm số \(f\left(x\right)=\left|g\left(x\right)\right|\)có \(4\)điểm cực trị thì phương trình \(g\left(x\right)=0\)có hai nghiệm phân biệt khác \(\pm1\).
\(g\left(x\right)=0\Leftrightarrow\frac{x}{x^2+x+1}=\frac{m}{3}\)
\(lim_{x\rightarrow-\infty}\frac{x}{x^2+x+1}=0,lim_{x\rightarrow+\infty}\frac{x}{x^2+x+1}=0\)
\(g\left(-1\right)=-1,g\left(1\right)=\frac{1}{3}\)
Suy ra BBT của hàm \(\frac{x}{x^2+x+1}\).
Từ đó suy ra để phương trình \(\frac{x}{x^2+x+1}\)có hai nghiệm phân biệt thì
\(\orbr{\begin{cases}0< \frac{m}{3}< \frac{1}{3}\\-1< \frac{m}{3}< 0\end{cases}}\Leftrightarrow m\in\left\{-2,-1\right\}\)(vì \(m\)nguyên)
Chọn A.