K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AT
12 tháng 7 2021
a) \(\left\{{}\begin{matrix}2x-3y=11\\5x-4y=3\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}10x-15y=55\left(1\right)\\10x-8y=6\left(2\right)\end{matrix}\right.\)
Lấy \(\left(1\right)-\left(2\right)\Rightarrow-7y=49\Rightarrow y=-7\Rightarrow2x=11+3\left(-7\right)=-10\)
\(\Rightarrow x=-5\)
b) đề nãy chỉ có 1 pt x,y không thể tính x,y được
c) bạn viết đề rõ ra chứ mờ quá đọc ko được
26 tháng 8 2021
Bài 3:
a: Ta có: ΔABC vuông tại A
nên \(\widehat{B}+\widehat{C}=90^0\)
hay \(\widehat{B}=60^0\)
Xét ΔABC vuông tại A có
\(AB=AC\cdot\tan30^0\)
\(=\dfrac{10\sqrt{3}}{3}\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow BC=\dfrac{20\sqrt{3}}{3}\left(cm\right)\)
TK
4 tháng 12 2021
1/
Để hàm số trên đồng biến
Thì m-1 > 0 ⇔ m>1
2/
a,<bạn tự vẽ>
b,Theo phương trình hoành độ giao điểm
\(2x=-x+3\Leftrightarrow3x=3\Leftrightarrow x=1\)
Thay x=1 vào y=2x
y=2.1=2
Vậy tọa độ giao điểm A là (1;2)
3/ Để (d) đi qua điểm M (1;-2)
Thì x=1 và y=-2
Thay x=1 và y=-2 vào (d)
\(-2=a\cdot1+1\Leftrightarrow a=-3\)
vậy ....
4 tháng 12 2021
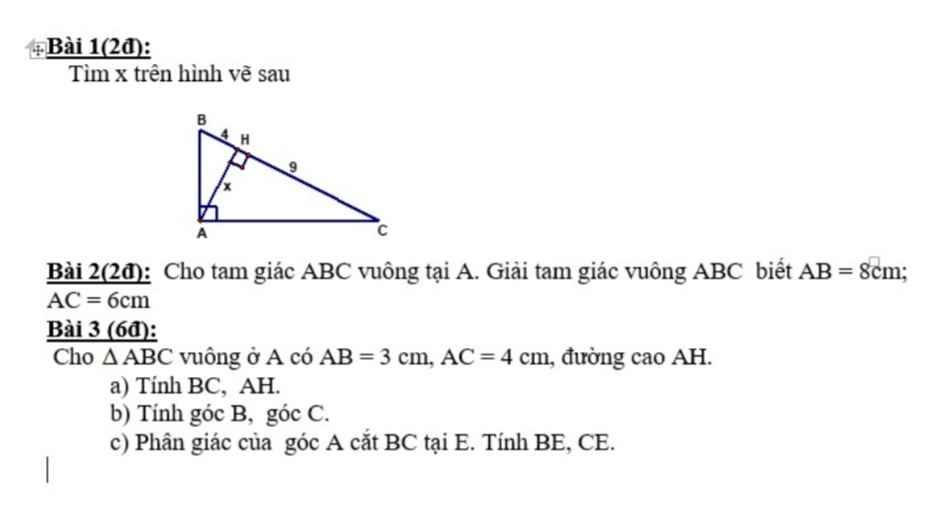
Bài 1:
Để hàm số bậc nhất \(y=\left(m-1\right)x+3\) đồng biến.
=> \(m-1>0.\)
<=> \(m>1.\)
Bài 2:
b) Xét phương trình hoành độ giao điểm của 2 hàm số trên ta có:
\(\text{2x = -x + 3.}\)
<=> \(\text{2x + x - 3= 0.}\)
<=> \(\text{3x - 3 = 0.}\)
<=> \(x=1.\)
=> \(y=2.\)
Vậy A(1; 2).
Bài 3:
Vì (d) đi qua điểm M(1; -2).
=> -2 = a. 1 + 1.
<=> a = -3.
Vậy a = -3.
AH
Akai Haruma
Giáo viên
30 tháng 10 2021
Bài 1:
Áp dụng HTL trong tam giác vuông:
$AH^2=BH.CH$
$\Leftrightarrow x^2=4.9=36$
$\Rightarrow x=6$ (do $x>0$)
AH
Akai Haruma
Giáo viên
30 tháng 10 2021
Bài 2:
Áp dụng định lý Pitago:
$BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10$ (cm)
$\sin B=\frac{AC}{BC}=\frac{6}{10}=\frac{3}{5}$
$\Rightarrow \widehat{B}=36,87^0$
$\widehat{C}=90^0-\widehat{B}=90^0-36,87^0=53,13^0$
DN
2
8 tháng 11 2021
Bài 4:
\(a,A=\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}}\\ P=A:B=\dfrac{\sqrt{x}+1}{\sqrt{x}}\cdot\dfrac{x-1}{\sqrt{x}+1}=\dfrac{x-1}{\sqrt{x}}\\ b,P\sqrt{x}=m-\sqrt{x}+x\\ \Leftrightarrow x-1=m-\sqrt{x}+x\\ \Leftrightarrow m=\sqrt{x}-1\)
21 tháng 8 2021
Bài 1:
a: Xét tứ giác NPIK có
\(\widehat{NKP}=\widehat{NIP}\left(=90^0\right)\)
Do đó: NPIK là tứ giác nội tiếp
hay N,P,I,K cùng thuộc 1 đường tròn
b: Xét tứ giác MKHI có
\(\widehat{MKH}+\widehat{MIH}=180^0\)
Do đó: MKHI là tứ giác nội tiếp
hay M,K,H,I cùng thuộc 1 đường tròn
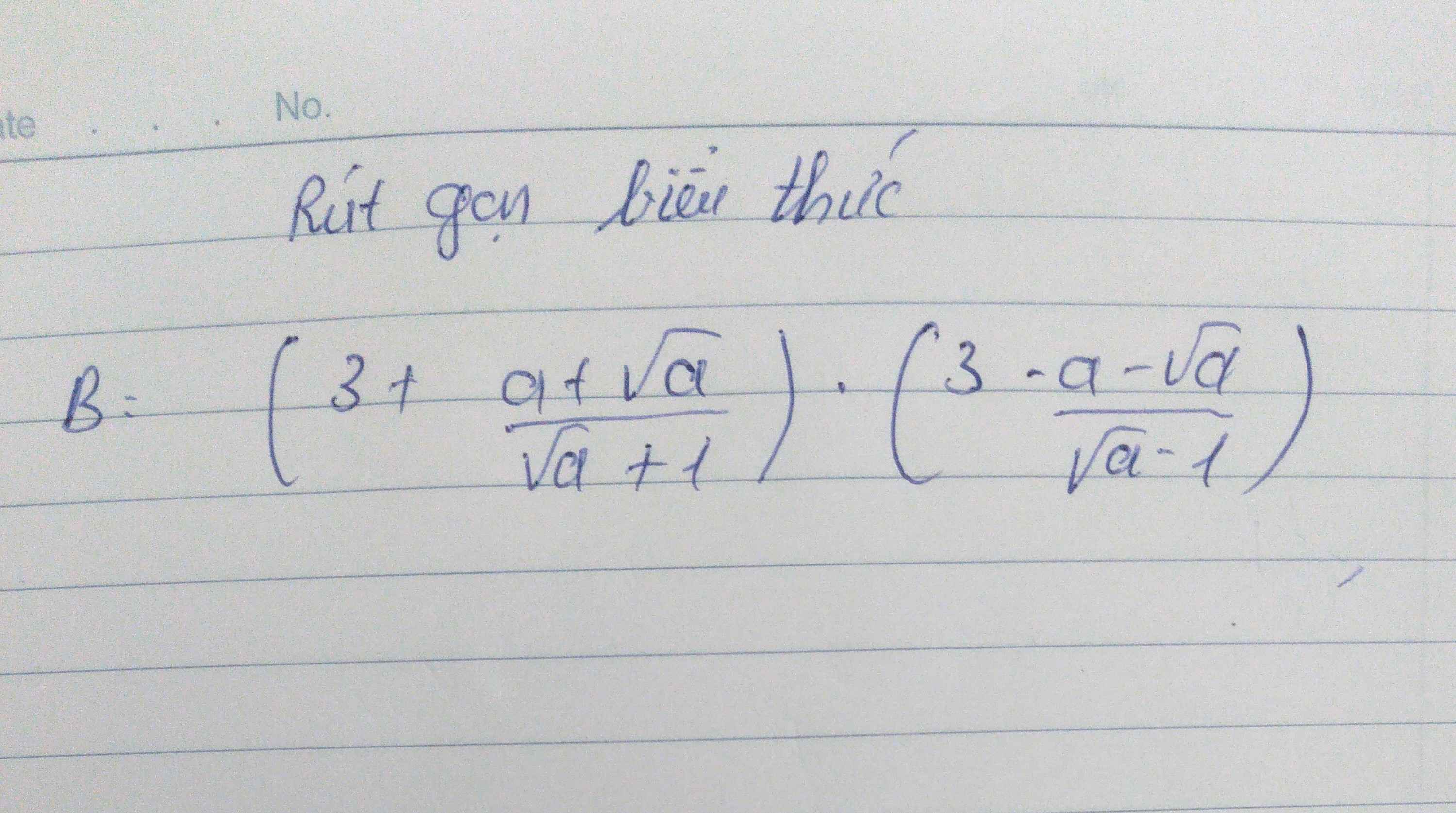
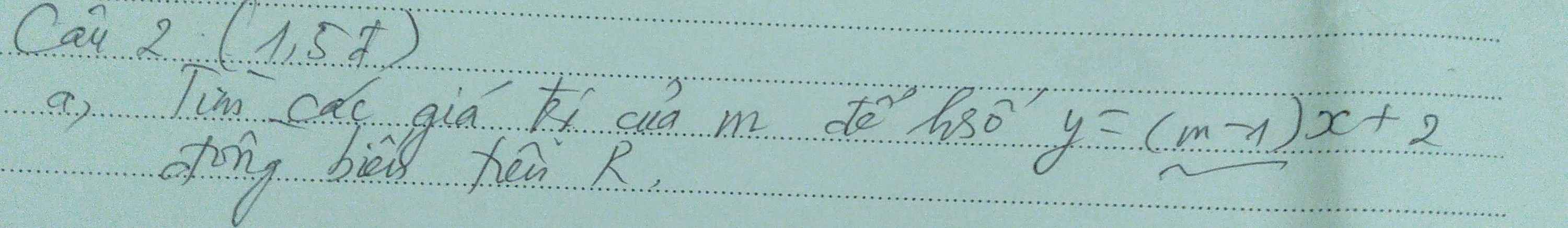
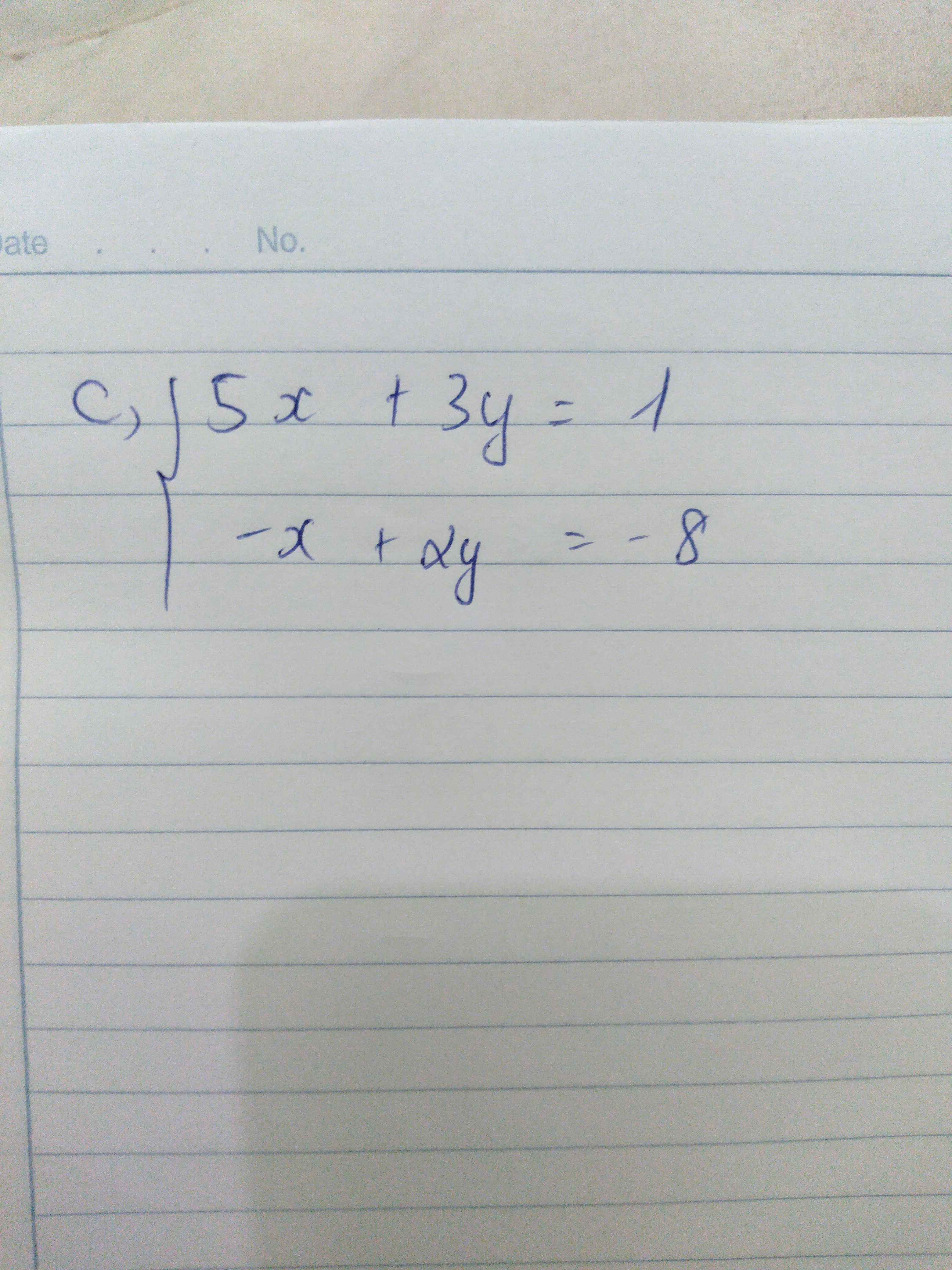
\(B=\left(3+\dfrac{a+\sqrt{a}}{\sqrt{a}+1}\right)\left(3-\dfrac{a-\sqrt{a}}{\sqrt{a}-1}\right)\left(a\ge0,a\ne1\right)\)
\(=\left(3+\dfrac{\sqrt{a}\left(\sqrt{a}+1\right)}{\sqrt{a}+1}\right)\left(3-\dfrac{\sqrt{a}\left(\sqrt{a}-1\right)}{\sqrt{a}-1}\right)=\left(3+\sqrt{a}\right)\left(3-\sqrt{a}\right)=9-a\)
Để hàm số \(y=\left(m-1\right)x+2\) đồng biến trên R thì \(m-1>0\Rightarrow m>1\)
Câu 2:
Để hàm số y=(m-1)x+2 đồng biến trên R thì m-1>0
hay m>1