Tìm x,y thuộc N biết x2 +2x+13=y2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
21 tháng 2 2019
Đáp án A
Ta có, giả thiết
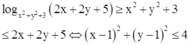
là miền trong đường tròn tâm I(1;1) bán kính R1 = 2
Và
CM
13 tháng 4 2019
c)Ta có: x2 + y2 – 2x + 4y + 5 = (x2 – 2x + 1) + (y2 + 4y + 4)
= (x – 1)2 + (y + 2)2
Vậy (x – 1)2 + (y + 2)2 = 0 ⇒ x – 1 = 0 hay y + 2 = 0
⇒ x = 1 hoặc y = -2
1
rút gọn P=2/x-(x2/(x2-xy)+(x2-y2)/xy-y2/(y2-xy)):(x2-xy+y2)/(x-y)
r tìm gt P với |2x-1|=1 ; |y+1|=1/2
1
13 tháng 12 2015
xy+2x+y-13=0
x(y+2)+y+2=15
x(y+2)+(y+2)=15
(x+1)(y+2)=15
=>
| x+1 | 1 | 3 | 5 | 15 |
| x | 0 | 2 | 4 | 14 |
| y+2 | 15 | 5 | 3 | 1 |
| y | 13 | 3 | 1 |
.
.
.
12 tháng 7 2018
a, (x^2 -2x+1)+(y^2 +6y+9) =0
(x-1)^2 +(y+3)^2 =0
Do đó: x-1=0 và y+3=0
Vậy x=1 và y=-3
b, x^2 +y^2 +1=xy+x+y
2x^2 +2y^2 +2=2xy+2x+2y
2x^2 +2y^2 -2xy-2x-2y +2=0
(x^2 -2x+1)+(y^2 -2y+1)+ (x^2 +y^2 -2xy)=0
(x-1)^2 +(y-1)^2 +(x-y)^2 =0
Suy ra: x-1=0, y-1=0 và x-y=0
Vậy x=1,y=1
c,5x^2 - 4x-2xy+y^2 +1=0
(4x^2 -4x+1)+(x^2 -2xy+y^2 )=0
(2x-1)^2 +(x-y)^2 =0
Do đó: 2x-1 =0 và x=y suy ra: x=0,5 và x=y
Vậy x=y=0,5
\(x^2+2x+13=y^2\)
\(\Rightarrow4x^2+8x+52=4y^2\)
\(\Rightarrow\left(2x+2\right)^2+48=4y^2\)
\(\Rightarrow\left(2x+2\right)^2-4y^2=-48\)
\(\Rightarrow\left(2x-2y+2\right)\left(2x+2y+2\right)=-48\)
\(\Rightarrow\left(x-y+1\right)\left(x+y+1\right)=-12\) (1)
Ta có: \(x-y+1+x+y+1=2x+2⋮2\)
Do đó: x - y + 1 và x + y + 1 cùng tĩnh chẵn lẻ.
Mà \(x,y\in N\)nên \(x-y+1< x+y+1\) (2)
Từ (1) và (2) ta được: \(\hept{\begin{cases}x-y+1=-2\\x+y+1=6\end{cases}\Rightarrow\hept{\begin{cases}x-y=-3\\x+y=5\end{cases}\Rightarrow}}\hept{\begin{cases}x=1\\y=4\end{cases}}\) (thỏa mãn)
Vậy x = 1 và y = 4