Con lắc đơn dđđh trong thang máy đứng yên với gia tốc trọng trường g = 9.8 m/s với năng lượng dao động là 150 mJ, gốc thế năng là vị trí cân bằng quả nặng, đúng lúc vận tốc con lắc bằng không thì thang máy chuyển động nhanh dần đều đi lên gia tốc 2.5 m/s, con lắc sẽ tiếp tục dao động với năng lượng
A. 150 mJ
B. 188.2 mJ
C. 129.5 mJ
D. 111.7 mJ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HD
Hà Đức Thọ
Admin
27 tháng 3 2015
Thang máy chuyển động nhanh dần đều đi lên thì: \(g'=g+a=9,8+2,5=12,3\)m/s2
Khi vận tốc thang máy bằng 0 thì cơ năng con lắc bằng thế năng. Do vậy, gia tốc tăng lên g' thì thế năng cũng tăng lỉ lệ tương ứng, mà động năng bằng 0 nên cơ năng cũng tăng tỉ lệ như vậy.
Ta có: \(\frac{W'}{W}=\frac{g'}{g}=\frac{12,3}{9,8}\)
\(\Rightarrow W'=\frac{12,3}{9,8}.150=188,3J\)
Đáp án D.
![[IMG]](https://i.imgur.com/IIa9USo.png)
2 tháng 8 2016
Thang máy chuyển động nhanh dần đều đi lên thì :
\(g'=g+a=9,8+2,5=12,3\) m/s2
Khi vận tốc thang máy bằng 0 thì cơ năng con lắc bằng thế năng. Do vậy, gia tốc tăng lên g' thì thế năng cũng tăng lỉ lệ tương ứng, mà động năng bằng 0 nên cơ năng cũng tăng tỉ lệ như vậy.
Ta có : \(\frac{W'}{W}=\frac{g'}{g}=\frac{12,3}{9,8}\)
\(\Rightarrow W'=\frac{12,3}{9,8}.150=188,3J\)
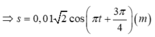
Gia tốc biểu kiến của con lắc trong thang máy là
\(\overrightarrow{g'} =\overrightarrow{g} -\overrightarrow{a} \)
Thang máy đứng yên: \(\overrightarrow{a} = 0; W= \frac{1}{2}kA^2= 0,5 m\omega^2g.(1) \)
Thang máy chuyển động nhanh dần đều đi lên gia tốc \(2,5 m/s\) => \(\overrightarrow{g} \uparrow \downarrow \overrightarrow{a} \)
=> \(g' = g-(-a)= g+a.\)
=> \(W' = \frac{1}{2}m\omega'^2.A^2.(2)\)
Chia (1) cho (2) ta có: \(\frac{W}{W'} = \frac{\omega ^2}{\omega'^2}= \frac{T'^2}{T^2}= \frac{g}{g'}= \frac{9,8}{12,3}=> W'= \frac{12,3.150}{9,8}=188,2mJ.\)
Chọn đáp án.B.188,2mJ.