Giải phương trình nghiệm nguyên: 2x^2-xy+7y^3=4880
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
1
DD
Đoàn Đức Hà
Giáo viên
17 tháng 6 2021
\(2x^2-y^2+xy-3x+3y-3=0\)
\(\Leftrightarrow2x^2-xy+x+2xy-y^2+y-4x+2y-2=1\)
\(\Leftrightarrow\left(2x-y+1\right)\left(x+y-2\right)=1\)
Từ đây bạn xét bảng giá trị và thu được kết quả cuối cùng là: \(\left(x,y\right)=\left(1,2\right)\).
TL
2
21 tháng 2 2016
bạn ơi, xem lại đề ra 1 chút, hình như có câu sai đề thì phải
XO
31 tháng 1 2022
Ta có \(3x^2+7y^2=210\Rightarrow7y^2=210-3x^2\le210\)
=> \(y^2\le30\Rightarrow y\in\left\{0;\pm1;\pm2;\pm3;\pm4;\pm5\right\}\)(vì \(y\in Z\)) (1)
Lại có \(7y^2=210-3x^2=3\left(70-x^2\right)⋮3\)
=> \(y⋮3\left(\text{vì(7;3) = 1}\right)\)(2)
Từ (1) (2) => y = \(\pm3\) => x = \(\pm\)7
Vậy các cặp (x;y) thỏa là (7;3) ; (7;-3) ; (-7; -3) ; (-7 ; 3)
25 tháng 5 2016
Ta có: nhân hai vế vs 2:
2x2+2y2+2xy=4x+2y
=> (x2-4x+4)+(x2+2xy+y2)+(y2-2y+1)=5
=> (x-2)2+(x+y)2+(y-1)2=5=02+12+22
Thử các trường hợp rồi giải ra nhé! Chúc bạn học tốt!
CM
10 tháng 6 2017
Điều kiện y ≠ 0
Hệ phương trình tương đương với x + y + x y = 7 ( 1 ) x x y + 1 = 12 ( 2 )
Từ (1) và x, y là số nguyên nên y là ước của x
Từ (2) ta có x là ước của 12
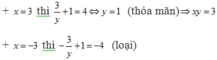
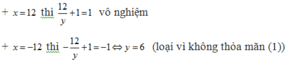
Vậy có duy nhất một nghiệm nguyên x = 3, y = 1 nên xy = 3
Đáp án cần chọn là: C
