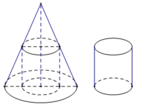
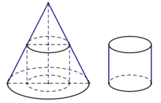
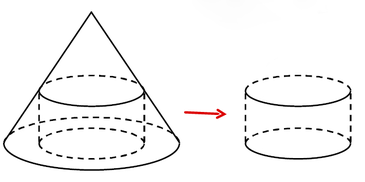
Từ một khúc gỗ hình trụ cao 15 cm, người ta tiện thành một khối gỗ hình nón với chiều cao giữ nguyên từ khúc gỗ ban đầu và đáy nón chính là đáy khúc gỗ hình trụ. Biết phần
gỗ bỏ đi có thể tích là 640r(cm). Tính thể tích khối gỗ hình nón đã tiện được.






Lời giải:
Gọi bán kính đáy khúc gỗ là $r$ (cm) thì:
Thể tích khúc gỗ:
$\pi r^2h=15\pi r^2$ (cm khối)
Thể tích hình nón:
$\frac{1}{3}\pi r^2h=5\pi r^2$ (cm khối)
Thể tích phần bỏ đi:
$15\pi r^2-5\pi r^2=640r$ (cm khối)
$10\pi r^2=640r$
$10\pi r=640$
$r=\frac{64}{\pi}$ (cm)
Thể tích khối nón: $5\pi r^2=5\pi.\frac{64^2}{\pi ^2}=\frac{20480}{\pi}$ (cm khối)
Nghe đề bài có vẻ sai sai. Nếu đề là $640\pi$ (cm khối) thì bạn cũng làm tương tự, $r=8$ (cm)